题目内容
2.若M为△ABC的重心,O为任意一点,$\overrightarrow{OA}$$+\overrightarrow{OB}$$+\overrightarrow{OC}$=n$\overrightarrow{OM}$,则n=( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 可作出图形,从而有$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}$,M为重心,从而有$\overrightarrow{AM}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,再根据向量减法的几何意义便可以得到$n\overrightarrow{OM}=\frac{n}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$,这样根据平面向量基本定理便可得到$\frac{n}{3}=1$,从而便可得出n的值.
解答 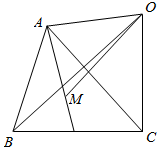 解:如图,
解:如图,
$\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{AM}$=$\overrightarrow{OA}+\frac{2}{3}[\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})]$=$\overrightarrow{OA}+\frac{1}{3}[(\overrightarrow{OB}-\overrightarrow{OA})+(\overrightarrow{OC}-\overrightarrow{OA})]$=$\frac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$;
∴$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=n\overrightarrow{OM}=\frac{n}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$;
∴$\frac{n}{3}=1$;
∴n=3.
故选D.
点评 考查向量加法、减法及数乘的几何意义,向量加法的平行四边形法则,以及平面向量基本定理.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | {3} | B. | {3.4} | C. | {3.4,5} | D. | {3.4,5,6} |
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |