题目内容
11.已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,$f(x)=\left\{\begin{array}{l}{2^{|x-1|}}-1,0<x≤2\\ \frac{1}{2}f(x-2),x>2\end{array}\right.$,则函数g(x)=2f(x)-1的零点个数为6.分析 函数g(x)=2f(x)-1的零点个数等于函数f(x)图象与直线y=$\frac{1}{2}$交点的个数,数形结合可得答案.
解答 解:函数g(x)=2f(x)-1的零点个数等于函数f(x)图象与直线y=$\frac{1}{2}$交点的个数,
∵函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,
当x>0时,$f(x)=\left\{\begin{array}{l}{2^{|x-1|}}-1,0<x≤2\\ \frac{1}{2}f(x-2),x>2\end{array}\right.$,
在同一坐标系画出函数的图象如下图所示,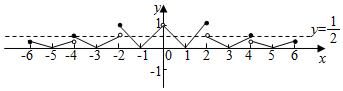
由图可得:函数f(x)图象与直线y=$\frac{1}{2}$有6个交点,
故答案为:6.
点评 本题考查的知识点是函数的奇偶性,函数的零点与方程根的关系,难度中档.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
19.集合A={x|lnx≥0},B={x|x2<9},则A∩B=( )
| A. | (1,3) | B. | [1,3) | C. | [1,+∞) | D. | [e,3) |



