题目内容
4.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则p的值为2或8.分析 求出M(5-$\frac{p}{2}$,4),代入抛物线方程得p2-10p+16=0,求出p.
解答 解:∵抛物线C方程为y2=2px(p>0),∴焦点F($\frac{p}{2}$,0),
设M(x,y),由抛物线性质|MF|=x+$\frac{p}{2}$=5,可得x=5-$\frac{p}{2}$,
因为圆心是MF的中点,所以根据中点坐标公式可得,圆心横坐标为$\frac{5-\frac{p}{2}+\frac{p}{2}}{2}$=$\frac{5}{2}$,
由已知圆半径也为$\frac{5}{2}$,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
即M(5-$\frac{p}{2}$,4),代入抛物线方程得p2-10p+16=0,所以p=2或p=8.
故答案为2或8.
点评 本题给出抛物线一条长度为5的焦半径MF,以MF为直径的圆交抛物线于点(0,2),求p的值,着重考查了抛物线的定义与简单几何性质、圆的性质和解直角三角形等知识,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
8.已知椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$,则以点$(2,\frac{3}{2})$为中点的弦所在的直线方程为( )
| A. | 8x-6y-7=0 | B. | 3x+4y=0 | C. | 3x+4y-12=0 | D. | 6x+8y-25=0 |
15.若-$\frac{π}{8}$<θ<0,则sinθ,cosθ,tanθ的大小关系为( )
| A. | sinθ<tanθ<cosθ | B. | tanθ<sinθ<cosθ | C. | tanθ<cosθ<sinθ | D. | sinθ<cosθ<tanθ |
9.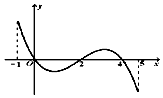 已知函数f(x)的定义域为[-1,5],部分对应值如下表,
已知函数f(x)的定义域为[-1,5],部分对应值如下表,
f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
①函数f(x)的极大值点为0,4;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④函数y=f(x)最多有3个零点.
其中正确命题的序号是( )
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,
已知函数f(x)的定义域为[-1,5],部分对应值如下表,| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | 2 | 2 | -1 |
①函数f(x)的极大值点为0,4;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④函数y=f(x)最多有3个零点.
其中正确命题的序号是( )
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
13.已知关于x的方程为x2+x+n2=0,若n∈[-1,1],则方程有实数根的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
14.已知i是虚数单位,复数$z=i+\frac{2}{1-i}$,则复数$\overline z$的虚部是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | -2 |