题目内容
8.已知椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$,则以点$(2,\frac{3}{2})$为中点的弦所在的直线方程为( )| A. | 8x-6y-7=0 | B. | 3x+4y=0 | C. | 3x+4y-12=0 | D. | 6x+8y-25=0 |
分析 设出弦的两个端点的坐标,代入椭圆方程,作差整理可得弦所在直线的斜率,写出直线方程的点斜式,化为一般式得答案.
解答 解:设弦的两个端点分别为A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{\frac{{{x}_{1}}^{2}}{16}+\frac{{{y}_{1}}^{2}}{9}=1①}\\{\frac{{{x}_{2}}^{2}}{16}+\frac{{{y}_{2}}^{2}}{9}=1②}\end{array}\right.$,
①-②得:$\frac{{{x}_{1}}^{2}-{{x}_{2}}^{2}}{16}=-\frac{{{y}_{1}}^{2}-{{y}_{2}}^{2}}{9}$,
即$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{16}=-\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{9}$,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{9({x}_{1}+{x}_{2})}{16({y}_{1}+{y}_{2})}=-\frac{9×4}{16×3}=-\frac{3}{4}$.
∴以点$(2,\frac{3}{2})$为中点的弦所在的直线方程为y-$\frac{3}{2}=-\frac{3}{4}(x-2)$,
整理得:3x+4y-12=0.
故选:C.
点评 本题考查椭圆的简单性质,训练了利用“点差法”求中点弦所在直线方程,是中档题.

练习册系列答案
相关题目
18.要得到函数$y=sin({2x+\frac{π}{3}})$的图象,只要将函数y=sinx的图象( )
| A. | 先向左平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{π}{6}$个单位,再将各点横坐标变为原来的2倍 | |
| C. | 先向左平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的$\frac{1}{2}$倍 | |
| D. | 先向右平移$\frac{π}{3}$个单位,再将各点横坐标变为原来的2倍 |
16.如图所示,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为( )


| A. | 36+6$\sqrt{10}$ | B. | 36+3$\sqrt{10}$ | C. | 54 | D. | 27 |
3.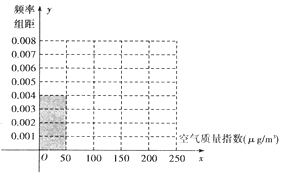 全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x、y的值,并完成频率分布直方图;
(Ⅱ)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
 全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
(Ⅱ)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
13.已知抛物线C:y2=2px(p>0),过其焦点F的直线l交抛物线C于点A、B,|AF|=3|BF|,则|AB|=( )
| A. | p | B. | $\frac{4}{3}p$ | C. | 2p | D. | $\frac{8}{3}p$ |