题目内容
18.已知菱形ABCD的边长为2,E为AB的中点,∠ABC=120°,则$\overrightarrow{DE}$•$\overrightarrow{BD}$的值为( )| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 根据棱形的性质以及向量的数量积公式计算即可.
解答 解:菱形ABCD的边长为2,∠ABC=120°,
∴AB=BD=AD=2,
∵E为AB的中点,
∴DE=$\frac{\sqrt{3}}{2}$AD=$\sqrt{3}$,∠EDB=30°,
∴$\overrightarrow{DE}$•$\overrightarrow{BD}$=-$\overrightarrow{DE}$•$\overrightarrow{DB}$=-$\sqrt{3}$×2×$\frac{\sqrt{3}}{2}$=-3,
故选:B
点评 本题考查了棱形的性质以及向量的数量积公式,属于基础题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=7,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
10.已知i为虚数单位,复数z满足(1+i)z=(1-i)2,则|z|为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
7.如图所示,已知$\overrightarrow{AC}=3\overrightarrow{BC}$,$\overrightarrow{OA}$=$\overrightarrow a$,$\overrightarrow{OB}$=$\overrightarrow b$,$\overrightarrow{OC}$=$\overrightarrow c$,则下列等式中成立的是( )
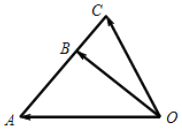

| A. | $\overrightarrow c=\frac{3}{2}\overrightarrow b-\frac{1}{2}\overrightarrow a$ | B. | $\overrightarrow c=2\overrightarrow b-\overrightarrow a$ | C. | $\overrightarrow c=2\overrightarrow a-\overrightarrow b$ | D. | $\overrightarrow c=\frac{3}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b$ |
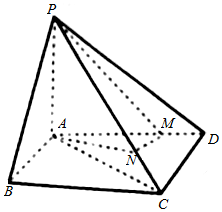 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,BC=AP=5,AB=3,AC=4,M,N分别在线段AD,CP上,且$\frac{AM}{MD}$=$\frac{PN}{NC}$=4.