题目内容
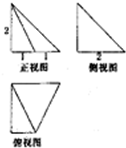某几何体的三视图如图所示，则其侧面的直角三角形的个数为（ ）| A、1 | B、2 | C、3 | D、4 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图判断几何体为四棱锥，且有一条侧棱与底面垂直，由俯视图得底面为直角梯形，画出其直观图，利用线面垂直的性质可证线线垂直，从而判断侧面直角三角形的个数．
解答：
解：由三视图知几何体为四棱锥，其直观图如图所示
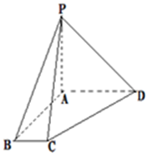
由正视图与侧视图知侧棱PA⊥底面ABCD，由俯视图知底面为直角梯形，AD∥BC，且BC⊥AB，
∴BC⊥平面PAB，BC⊥PB，
∴△PAB，△PBC，△PAD是直角三角形，
∵PC2=PA2+AC2=9，PD2=PA2+AD2=8，CD2=5，PD2≠PC2+CD2，△PCD不是直角三角形．
故选：C．
由正视图与侧视图知侧棱PA⊥底面ABCD，由俯视图知底面为直角梯形，AD∥BC，且BC⊥AB，
∴BC⊥平面PAB，BC⊥PB，
∴△PAB，△PBC，△PAD是直角三角形，
∵PC2=PA2+AC2=9，PD2=PA2+AD2=8，CD2=5，PD2≠PC2+CD2，△PCD不是直角三角形．
故选：C．
点评：本题考查由三视图判断几何体的特征性质，考查了线面垂直的判定与性质，解题的关键是由三视图判断线面及线线关系．
练习册系列答案
相关题目
已知A、B、C是单位圆上三个互不相同的点．若|
|=|
|，则
•
的最小值是（ ）
| AB |
| AC |
| AB |
| AC |
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
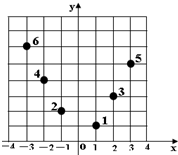如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列{an}（n∈N*）的前12项，如下表所示：| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A、501 | B、502 |
| C、503 | D、504 |
在△ABC中，AB=1，BC=2，
•
=
，则角B=（ ）
| BA |
| BC |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
复数z=
的虚部为（ ）
| 2 |
| -1+i |
| A、-1 | B、-i | C、1 | D、i |
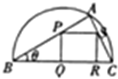如图所示，在直径为BC的半圆中，A是弧BC上一点，正方形PQRS内接于△ABC，若BC=a，∠ABC=θ，设△ABC的面积为Sl，正方形PQRS的面积为S2．