题目内容
7.已知角α的终边过点(-2,3),则sin2α=$-\frac{12}{13}$.分析 根据定义求出sinα,和cosα的值,利用二倍角公式可得sin2α的值.
解答 解:角α的终边过点(-2,3),根据三角函数的定义可知:sinα=$\frac{3}{\sqrt{13}}$,cosα=$\frac{-2}{\sqrt{13}}$,
则sin2α=2sinαcosα=$-2×\frac{2}{\sqrt{13}}×\frac{3}{\sqrt{13}}$=$-\frac{12}{13}$,
故答案为:$-\frac{12}{13}$.
点评 本题考查了三角函数的定义和二倍角公式的计算.属于基础知识考查.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.已知f(x)是定义在R上的奇函数,则f(0)=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 不存在 |
12.将函数$y=cos(2x+\frac{π}{6})$图象上的点$P(\frac{π}{4},t)$向右平移m(m>0)个单位长度得到点P',若P'位于函数y=cos2x的图象上,则( )
| A. | $t=-\frac{{\sqrt{3}}}{2}$,m的最小值为$\frac{π}{6}$ | B. | $t=-\frac{{\sqrt{3}}}{2}$,m的最小值为$\frac{π}{12}$ | ||
| C. | $t=-\frac{1}{2}$,m的最小值为$\frac{π}{6}$ | D. | $t=-\frac{1}{2}$,m的最小值为$\frac{π}{12}$ |
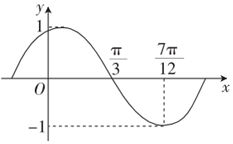 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),其部分图象如图所示.