题目内容
甲、乙两组各有三名同学，他们在一次测验中的成绩的茎叶图如图所示，如果分别从甲、乙两组中各随机挑选一名同学，则这两名同学的成绩之差的绝对值不超过3的概率为考点：古典概型及其概率计算公式
专题：概率与统计
分析：根据茎叶图中的数据，利用古典概率的概率公式，即可得到结论．
解答：
解：从甲、乙两组中各随机挑选一名同学共有3×3=9种选法．
若这两名同学的成绩之差的绝对值超过3的只有甲组是88，乙组数据是92，只有1种选法，
则这两名同学的成绩之差的绝对值不超过3的选法有9-1=8种选法，
故所求的概率为
，
故答案为：
．
若这两名同学的成绩之差的绝对值超过3的只有甲组是88，乙组数据是92，只有1种选法，
则这两名同学的成绩之差的绝对值不超过3的选法有9-1=8种选法，
故所求的概率为
| 8 |
| 9 |
故答案为：
| 8 |
| 9 |
点评：本题主要考查古典概率的概率公式的应用，比较基础．
练习册系列答案
相关题目
对于每个非零自然数n，抛物线y=x2-
x+
与x轴交于An、Bn两点，以AnBn表示这两点间的距离，则A1B1+A2B2+…+A2014B2014的值是（ ）
| 2n+1 |
| n2+n |
| 1 |
| n2+n |
A、
| ||
B、
| ||
C、
| ||
D、
|
点P（x，y）为不等式组
表示的平面区域上一点，则x+2y取值范围为（ ）
|
A、[-
| ||||
B、[-2，
| ||||
| C、[-1，2] | ||||
| D、[-2，2] |
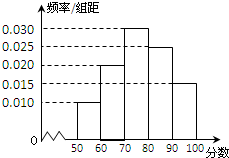某中学从某次考试成绩中抽取若干名学生的分数，并绘制成如图的频率分布直方图．样本数据分组为[50，60），[60，70），[70，80），[80，90），[90，100]．若用分层抽样的方法从样本中抽取分数在[80，100]范围内的数据16个，则其中分数在[90，100]范围内的样本数据有（ ）
正方体ABCD-A1B1C1D1的棱长为1，P为线段BC的中点，Q为线段CC1上的动点，过A，P，Q的平面截该正方体所得的截面记为S，则所有正确的命题是