题目内容
判断正误:
(1)若三棱锥的六条边都相等,则此三棱锥的三组对棱互相垂直;
(2)若三棱锥的三条侧棱与底面所成的角相等,则此三棱锥是正三棱锥. .
(1)若三棱锥的六条边都相等,则此三棱锥的三组对棱互相垂直;
(2)若三棱锥的三条侧棱与底面所成的角相等,则此三棱锥是正三棱锥.
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:(1)结合图形利用线面垂直的判定证明CD⊥平面AOB,再由线面垂直的性质得CD⊥AB,同理可证另两组对边也相互垂直,从而判断是正确的;
(2)结合图形,根据条件只能判定顶点在底面的射影为底面三角形的外心,而不能证明底面三角形为正三角形,从而判断是错误的.
(2)结合图形,根据条件只能判定顶点在底面的射影为底面三角形的外心,而不能证明底面三角形为正三角形,从而判断是错误的.
解答:
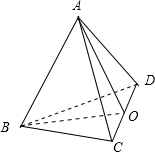
解:(1)如图:取CD的中点O,连接OA、OB,
∵AC=AD,∴AO⊥CD,
同理BO⊥CD,AO∩BO=O,∴CD⊥平面AOB,∴CD⊥AB,
同理AC⊥BD,AD⊥BC,
(2)如图设O为A在底面的射影,
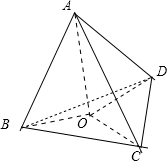
∵三条侧棱与底面所成的角相等,
∴∠OBA=∠OCA=∠ODA,∴OB=OC=OD即O为底面三角形的外心,底面三角形不一定为等边三角形,
∴三棱锥不一定为正三棱锥,
故答案为:(1)正确;(2)错误.
∵AC=AD,∴AO⊥CD,
同理BO⊥CD,AO∩BO=O,∴CD⊥平面AOB,∴CD⊥AB,
同理AC⊥BD,AD⊥BC,

(2)如图设O为A在底面的射影,

∵三条侧棱与底面所成的角相等,
∴∠OBA=∠OCA=∠ODA,∴OB=OC=OD即O为底面三角形的外心,底面三角形不一定为等边三角形,
∴三棱锥不一定为正三棱锥,
故答案为:(1)正确;(2)错误.
点评:本题考查了三棱锥的结构特征及正三棱锥的结构特征,判断正三棱锥要满足条件顶点在底面的射影是底面正三角形的中心.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学的成绩之差的绝对值不超过3的概率为
甲、乙两组各有三名同学,他们在一次测验中的成绩的茎叶图如图所示,如果分别从甲、乙两组中各随机挑选一名同学,则这两名同学的成绩之差的绝对值不超过3的概率为