题目内容
14. 如图所示,函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的一段图象过点(0,1)
如图所示,函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的一段图象过点(0,1)(1)求函数f(x)的解析式;
(2)将函数f(x)的图象上各点的纵坐标变为原来的$\frac{1}{2}$(横坐标不变),得到函数y=g(x)的图象,求y=g(x)的解析式及单调增区间.
分析 (1)由周期求出ω,由五点法作图求出φ的值,根据图象经过特殊点(0,1),求得A,可得函数的解析式.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,利用正弦函数的增区间求得g(x)的单调增区间.
解答 (1)结合函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的一段图象,
可得$\frac{2π}{ω}$=$\frac{11π}{12}$+$\frac{π}{12}$=π,∴ω=2.
再根据五点法作图可得2•(-$\frac{π}{12}$)+φ=0,求得φ=$\frac{π}{6}$.
再根据函数的图象经过点(0,1)可得Asin$\frac{π}{6}$=1,求得A=2,f(x)=2sin(2x+$\frac{π}{6}$).
(2)将函数f(x)的图象上各点的纵坐标变为原来的$\frac{1}{2}$(横坐标不变),
得到函数y=g(x)=sin(2x+$\frac{π}{6}$)的图象,
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,
故函数g(x)的单调增区间为$[kπ-\frac{π}{3},\;\;kπ+\frac{π}{6}]$(k∈Z).
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,根据图象经过特殊点(0,1),求得A,正弦函数的增区间,函数y=Asin(ωx+φ)的图象变换规律,求函数的解析式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | -3 | B. | -5 | C. | -6 | D. | -14 |
2.下列各数中最大的数为( )
| A. | 101111(2) | B. | 1210(3) | C. | 112(8) | D. | 69(12) |
19.复数z=$\frac{2}{1-i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.某四棱锥的三视图如图所示,则该四棱锥的侧面积是( )
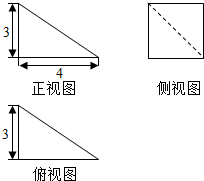

| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
3.下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是( )
| A. | y=2x | B. | y=$\sqrt{x}$ | C. | y=|x| | D. | y=-x2+1 |