题目内容
19.复数z=$\frac{2}{1-i}$(i为虚数单位)在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、复数的几何意义即可得出.
解答 解:$z=\frac{2}{1-i}=1+i$,在复平面内复数z对应点的坐标为(1,1),在第一象限.
故选:A.
点评 本题考查了复数的运算法则、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.函数y=cos($\frac{π}{2}$-x)sin($\frac{π}{2}$+x)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
8.执行如图所示的程序框图,若p=0.9,则输出的n为( )


| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
9.下列各角中,与50°的角终边相同的角是( )
| A. | -310° | B. | -50° | C. | 140° | D. | 40° |
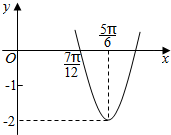 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1. 如图所示,函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的一段图象过点(0,1)
如图所示,函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的一段图象过点(0,1)