题目内容
已知函数f(x)=ln(x+1)+aln(1-x)(a∈R)的图象关于原点对称.
(1)求定义域;
(2)求a的值;
(3)若g(x)=ef(x)-
有零点,求m的取值范围.
(1)求定义域;
(2)求a的值;
(3)若g(x)=ef(x)-
| 1-m |
| 2+m |
考点:奇偶性与单调性的综合,函数的定义域及其求法,函数的零点
专题:函数的性质及应用
分析:(1)利用对数函数的真数大于0,得到不等式组即可求定义域;
(2)利用函数是奇函数,即可求出a的值;
(3)若g(x)=ef(x)-
有零点,求m的取值范围.
(2)利用函数是奇函数,即可求出a的值;
(3)若g(x)=ef(x)-
| 1-m |
| 2+m |
解答:
解:(1)函数f(x)=ln(x+1)+aln(1-x)有意义,
必有:
,解得x∈(-1,1)
函数的定义域为:(-1,1)…(3分)
(2)函数f(x)=ln(x+1)+aln(1-x)(a∈R)的图象关于原点对称,函数是奇函数,
函数的定义域为:(-1,1),
所以f(x)=-f(-x),即ln(x+1)+aln(1-x)=-ln(-x+1)-aln(1+x)
∴a=-1 …(8分)
(3)函数f(x)=ln(x+1)-ln(1-x)=ln
,
由题意:ef(x)-
=0,在x∈(-1,1)上有解,
即:
=
,∴x=-
m-
∈(-1,1).解得:-2<m<1
∴m∈(-2,1)…(15分)
必有:
|
函数的定义域为:(-1,1)…(3分)
(2)函数f(x)=ln(x+1)+aln(1-x)(a∈R)的图象关于原点对称,函数是奇函数,
函数的定义域为:(-1,1),
所以f(x)=-f(-x),即ln(x+1)+aln(1-x)=-ln(-x+1)-aln(1+x)
∴a=-1 …(8分)
(3)函数f(x)=ln(x+1)-ln(1-x)=ln
| 1+x |
| 1-x |
由题意:ef(x)-
| 1-m |
| 2+m |
即:
| 1+x |
| 1-x |
| 1-m |
| 2+m |
| 2 |
| 3 |
| 1 |
| 3 |
∴m∈(-2,1)…(15分)
点评:本题考查函数的单调性与函数的奇偶性的综合应用,考查基本知识.

练习册系列答案
相关题目
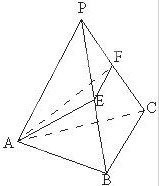 如图,设正三棱锥P-ABC的侧棱长为1,∠APB=30°,E、F分别是BP、CP上的一点,求△AEF周长的最小值.
如图,设正三棱锥P-ABC的侧棱长为1,∠APB=30°,E、F分别是BP、CP上的一点,求△AEF周长的最小值.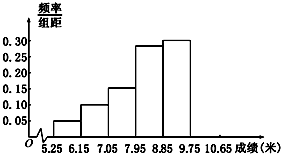 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.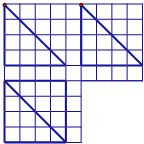 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为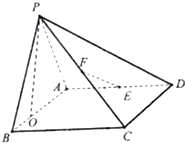 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点