题目内容
已知集合P={x，y，1}，M={x，x2，xy}，且P⊆M，M⊆P，求实数x、y的值．
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：据集合相等的定义，集合集合P={x，y，1}，M={x，x2，xy}，中元素对应相等，由此我们可以分类讨论构造不同的方程组，然后根据集合元素的性质排除不满足情况的答案，即可得到结论．
解答：
解：∵P⊆M，M⊆P，∴P=M，
∵集合P={x，y，1}，M={x，x2，xy}，
∴x2=1，xy=y或x2=y，xy=1，
当x2=1，xy=y时，
x=±1，
若x=1，此时x=x2，
这与集合元素的互异性矛盾
故不满足题目要求
若x=-1，则y=0
当x2=y，xy=1，x=1，此时x=x2，
这与集合元素的互异性矛盾
故不满足题目要求
综上x=-1，y=0．
∵集合P={x，y，1}，M={x，x2，xy}，
∴x2=1，xy=y或x2=y，xy=1，
当x2=1，xy=y时，
x=±1，
若x=1，此时x=x2，
这与集合元素的互异性矛盾
故不满足题目要求
若x=-1，则y=0
当x2=y，xy=1，x=1，此时x=x2，
这与集合元素的互异性矛盾
故不满足题目要求
综上x=-1，y=0．
点评：本题考查的知识点是集合相等的定义，其中易忽略集合元素的互异性，而产生增根．
练习册系列答案
应用题作业本系列答案
相关题目
已知f（x）是R上的偶函数，对任意的x1，x2∈[0，+∞）（x1≠x2），有
＜0，则f（-2），f（-π），f（3）的大小关系是（ ）
| f(x2)-f(x1) |
| x2-x1 |
| A、f（-π）＞f（-2）＞f（3） |
| B、f（3）＞f（-π）＞f（-2） |
| C、f（-2）＞f（3）＞f（-π） |
| D、f（-π）＞f（3）＞f（-2） |
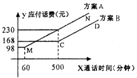电信局为满足不同客户的需要，设有A、B两种优惠方案，这两种方案应付话费（元）与通话时间（分钟）之间的关系如图（MN∥CD），若通话时间为500分钟，则应选择哪种方案更优惠（ ）| A、方案A | B、方案B |
| C、两种方案一样优惠 | D、不能确定 |
在空间坐标中，O为坐标原点，A（1，2，3），则|OA|等于（ ）
A、
| ||
B、
| ||
C、2
| ||
D、
|