题目内容
已知椭圆的中心在原点,对称轴是坐标轴,直线y=
x与椭圆在第一象限的交点是M,M在x轴上的射影恰好是椭圆的右焦点F2,另一个焦点是F1.
(1)求椭圆的离心率;
(2)若
•
=2,求椭圆的方程;
(3)在(2)的条件下,直线l经过左焦点F1,且与椭圆相交于P,Q两点,求△F2PQ面积的最大值.
| ||
| 2 |
(1)求椭圆的离心率;
(2)若
| MF1 |
| MF2 |
(3)在(2)的条件下,直线l经过左焦点F1,且与椭圆相交于P,Q两点,求△F2PQ面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设出椭圆的方程,根据题意,得出点M的坐标,结合直线方程,求出离心率e;
(2)由
•
=2得方程①,e=
得方程②,b2=a2-c2③,①②③组成方程组,求出a2、b2即可;
(3)讨论直线l的斜率不存在时,求得△F2PQ的面积,直线l的斜率存在时,
设出直线方程y=k(x+2),与椭圆方程联立,求出△F2PQ的面积,由此求出△F2PQ面积的最大值.
(2)由
| MF1 |
| MF2 |
| ||
| 2 |
(3)讨论直线l的斜率不存在时,求得△F2PQ的面积,直线l的斜率存在时,
设出直线方程y=k(x+2),与椭圆方程联立,求出△F2PQ的面积,由此求出△F2PQ面积的最大值.
解答:
解:(1)设椭圆的方程是
+
=1(a>b>0),
由题意,点M的横坐标为c,纵坐标为
,
∴
c=
,
转化为
c=
,
即
=1-(
)2,
∴e2+
e-1=0,
解得e=
(负根舍去);
(2)∵M(c,
),∴
=(-2c,-
),
=(0,-
);
∴
•
=
=2①,
又∵e=
=
,
∴c=
a②,
由c2=a2-b2③,
①②③组成方程组,解得a2=8,b2=4,
∴椭圆的方程为
+
=1;
(3)当直线l的斜率不存在时,易求得P(-2,
),Q(-2,-
),△F2PQ的面积为4
;
当直线l的斜率存在时,设方程为y=k(x+2),
由代入椭圆方程得((1+2k2)x2+8k2x+(8k2-8)=0,
设P(x1,y1),Q(x2,y2),
则x1+x2=-
,x1x2=
,
∴△F2PQ的面积为
S△F2PQ=S△PF1F2+S△QF1F2
=
•|F1F2|•|y1-y2|
=2k|x1-x2|
=2k•
=4
•
<4
;
综上,△F2PQ面积的最大值为4
.
| x2 |
| a2 |
| y2 |
| b2 |
由题意,点M的横坐标为c,纵坐标为
| b2 |
| a |
∴
| ||
| 2 |
| b2 |
| a |
转化为
| ||
| 2 |
| a2-c2 |
| a |
即
| ||
| 2 |
| c |
| a |
| c |
| a |
∴e2+
| ||
| 2 |
解得e=
| ||
| 2 |
(2)∵M(c,
| b2 |
| a |
| MF1 |
| b2 |
| a |
| MF2 |
| b2 |
| a |
∴
| MF1 |
| MF2 |
| b4 |
| a2 |
又∵e=
| c |
| a |
| ||
| 2 |
∴c=
| ||
| 2 |
由c2=a2-b2③,
①②③组成方程组,解得a2=8,b2=4,
∴椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(3)当直线l的斜率不存在时,易求得P(-2,
| 2 |
| 2 |
| 2 |
当直线l的斜率存在时,设方程为y=k(x+2),
由代入椭圆方程得((1+2k2)x2+8k2x+(8k2-8)=0,
设P(x1,y1),Q(x2,y2),
则x1+x2=-
| 8k2 |
| 1+2k2 |
| 8k2-8 |
| 1+2k2 |
∴△F2PQ的面积为
S△F2PQ=S△PF1F2+S△QF1F2
=
| 1 |
| 2 |
=2k|x1-x2|
=2k•
| (x1+x2)2-4x1x2 |
=4
| 2 |
|
| 2 |
综上,△F2PQ面积的最大值为4
| 2 |
点评:本题考查了直线与椭圆的综合应用问题,也考查了椭圆的离心率和求椭圆的标准方程的应用问题,是综合题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知函数f(x)的定义域为R,且对任意x∈R都有f(x)=f(x-1)+f(x+1),若f(-1)=2,f(1)=3则f(2012)+f(-2012)=( )
| A、-5 | B、-10 |
| C、5055 | D、5060 |
设等差数列{an}的前n项和为Sn,已知a1=-11,a3+a7=-6,当Sn取得最小值是,n=( )
| A、5 | B、6 | C、7 | D、8 |
 如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )
如图,在一个边长为2的正方形中随机撒入200粒的豆子,恰有120粒落在阴影区域里,则该阴影部分的面积约为( )A、
| ||
B、
| ||
C、
| ||
D、
|
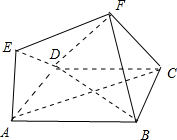 如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2
如图所示,已知在多面体ABCDEF中,底面是正方形,EA⊥平面ABCD,EF∥AC且AC=2EF,AB=2AE=2