题目内容
设定义在R上的奇函数y=f(x),满足对任意t∈R,都有f(t)=f(1-t),且x∈ 时,f(x)=-x2,则f(3)+f
时,f(x)=-x2,则f(3)+f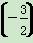 的值等于( )
的值等于( )
A.-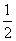 B.-
B.-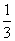
C.-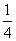 D.-
D.-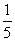
C解析 由f(t)=f(1-t),
得f(1+t)=f(-t)=-f(t).
所以f(2+t)=-f(1+t)=f(t),
所以f(x)的周期为2.
又f(1)=f(1-1)=f(0)=0,
所以f(3)+f
=f(1)+f =0-
=0- 2
2
=-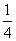 .故选C.
.故选C.

练习册系列答案
相关题目
 例如:34=3,(-2)4=4,则函数f(x)=x2(2x-x2)的最大值为________.
例如:34=3,(-2)4=4,则函数f(x)=x2(2x-x2)的最大值为________.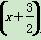 f(x)=2 014,且当x∈
f(x)=2 014,且当x∈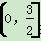 时,f(x)=log2(2x+1),则f(-2 015)+f(2 013)=________.
时,f(x)=log2(2x+1),则f(-2 015)+f(2 013)=________.
 +
+ 的最小值是________.
的最小值是________.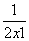 :
: