题目内容
已知函数f(x)为定义在R上的奇函数,当x≥0时,都有f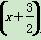 f(x)=2 014,且当x∈
f(x)=2 014,且当x∈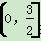 时,f(x)=log2(2x+1),则f(-2 015)+f(2 013)=________.
时,f(x)=log2(2x+1),则f(-2 015)+f(2 013)=________.
-2 014
解析 因为函数f(x)为奇函数且f(0)有定义,故f(0)=0,且f(-2 015)=-f(2 015).
当x≥0时,由f f(x)=2 014,可得f
f(x)=2 014,可得f =
= ,故f(x+3)=
,故f(x+3)= =f(x).
=f(x).
可得f(2 015)=f(3×671+2)=f(2),
f(2 013)=f(3×671)=f(0).
 故f(-2 015)=-2 014.
故f(-2 015)=-2 014.
综上,f(-2 015)+f(2 013)
=-2 014+0=-2 014.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知函数y=f(x)的图象是连续不间断的曲线,且有如下的对应值:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 124.4 | 35 | -74 | 14.5 | -56.7 | -123.6 |
则函数y=f(x)在区间[1,6]上的零点至少有( )
A.2个 B.3个
C.4个 D.5个
 的定义域是________.
的定义域是________.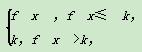 取函数f(x)=2-|x|.当k=
取函数f(x)=2-|x|.当k=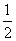 时,函数fk(x)的单调递增区间为( )
时,函数fk(x)的单调递增区间为( ) 时,f(x)=-x2,则f(3)+f
时,f(x)=-x2,则f(3)+f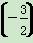 的值等于( )
的值等于( )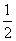 B.-
B.-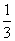
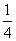 D.-
D.-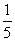

 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )