题目内容
已知函数f(x)=x3+ax2+bx+c,点P(1,f(1))在函数y=f(x)的图象上,过P点的切线方程为y=3x+1.
(1)若y=f(x)在x=-2时有极值,求f(x)的解析式;
(2)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围;
(3)在(1)的条件下是否存在实数m,使得不等式f(x)≥m在区间[-2,1]上恒成立,若存在,试求出m的最大值,若不存在,试说明理由.
(1)若y=f(x)在x=-2时有极值,求f(x)的解析式;
(2)若函数y=f(x)在区间[-2,1]上单调递增,求实数b的取值范围;
(3)在(1)的条件下是否存在实数m,使得不等式f(x)≥m在区间[-2,1]上恒成立,若存在,试求出m的最大值,若不存在,试说明理由.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由于函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,所以f(1)=4,f′(1)=3,又因为y=f(x)在x=-2时有极值,所以f′(-2)=0,列三个方程解之即可;
(2)由于函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,所以 f′(1)=3,所以2a=-b,欲使函数y=f(x)在区间[-2,1]上单调递增,只需f′(x)=3x2-bx+b≥0在区间[-2,1]上恒成立,转化为b≥
在区间[-2,1]上恒成立,利用函数性质求此函数的最大值即可;
(3)由(1)可知,f(x)解析式,由于不等式f(x)≥m在区间[-2,1]上恒成立,须使[f(x)]min≥m(x∈[-2,1]),再由导数与单调性关系即可得到,f(x)在区间[-2,1]上最小值,继而可以得到m的最大值.
(2)由于函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,所以 f′(1)=3,所以2a=-b,欲使函数y=f(x)在区间[-2,1]上单调递增,只需f′(x)=3x2-bx+b≥0在区间[-2,1]上恒成立,转化为b≥
| 3x2 |
| x-1 |
(3)由(1)可知,f(x)解析式,由于不等式f(x)≥m在区间[-2,1]上恒成立,须使[f(x)]min≥m(x∈[-2,1]),再由导数与单调性关系即可得到,f(x)在区间[-2,1]上最小值,继而可以得到m的最大值.
解答:
解:(1)由于函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,
所以f(1)=4,f′(1)=3,
又因为y=f(x)在x=-2时有极值,所以f′(-2)=0,
由于f′(x)=3x2+2ax+b
则
,解得a=2,b=-4,c=5
∴f(x)=x3+2x2-4x+5
(2)∵函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,
∴f′(1)=3,∴2a=-b
∴f′(x)=3x2-bx+b
依题意欲使函数y=f(x)在区间[-2,1]上单调递增,只需f′(x)=3x2-bx+b≥0在区间[-2,1]上恒成立
即b≥
在区间[-2,1]上恒成立
由于
≤0,则b≥0时,函数y=f(x)在区间[-2,1]上单调递增;
(3)假设在(1)的条件下存在实数m,使得不等式f(x)≥m在区间[-2,1]上恒成立,
由(1)知,f(x)=x3+2x2-4x+5,则f′(x)=3x2+4x-4=(x+2)(3x-2),
令f′(x)<0,则-2<x<
,则f(x)在区间[-2,
]上递减,在(
,1]上递增,
则[f(x)]min=f(
)=(
)3+2×(
)2-4×
+5=
若使f(x)≥m在区间[-2,1]上恒成立,须使[f(x)]min≥m(x∈[-2,1]),
则m≤
,则m的最大值为
.
所以f(1)=4,f′(1)=3,
又因为y=f(x)在x=-2时有极值,所以f′(-2)=0,
由于f′(x)=3x2+2ax+b
则
|
∴f(x)=x3+2x2-4x+5
(2)∵函数f(x)=x3+ax2+bx+c在点P(1,f(1))处的切线方程为y=3x+1,
∴f′(1)=3,∴2a=-b
∴f′(x)=3x2-bx+b
依题意欲使函数y=f(x)在区间[-2,1]上单调递增,只需f′(x)=3x2-bx+b≥0在区间[-2,1]上恒成立
即b≥
| 3x2 |
| x-1 |
由于
| 3x2 |
| x-1 |
(3)假设在(1)的条件下存在实数m,使得不等式f(x)≥m在区间[-2,1]上恒成立,
由(1)知,f(x)=x3+2x2-4x+5,则f′(x)=3x2+4x-4=(x+2)(3x-2),
令f′(x)<0,则-2<x<
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
则[f(x)]min=f(
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 145 |
| 27 |
若使f(x)≥m在区间[-2,1]上恒成立,须使[f(x)]min≥m(x∈[-2,1]),
则m≤
| 145 |
| 27 |
| 145 |
| 27 |
点评:本题考察了导数的几何意义,利用导数求函数极值,利用导数解决已知函数单调性求参数范围问题的方法,考查了转化化归的思想方法.

练习册系列答案
相关题目
函数f(x)=ax-1+3(a>0且a≠1)的图象过定点P,且点P在直线mx+ny-3=0(m>0且n>0)上,则
+
的最小值是( )
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、25 |
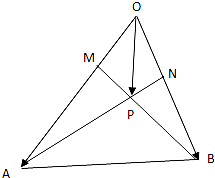 如图,在△OAB中,
如图,在△OAB中,