题目内容
（1）经计算发现：
+
＜2
，
+
＜2
，
+
＜2
，
试写出一个使
+
≤2
成立的正实数a，b满足的条件，并给出证明；
（2）若不等式
+
+
+
≤m
对任意的正实数a，b，c，d恒成立，
求实数m的取值范围．
| 7 |
| 15 |
| 11 |
| 5.5 |
| 16.5 |
| 11 |
3-
|
19+
|
| 11 |
试写出一个使
| a |
| b |
| 11 |
（2）若不等式
| a |
| b |
| c |
| d |
| a+b+c+d |
求实数m的取值范围．
考点：柯西不等式在函数极值中的应用
专题：综合题,不等式的解法及应用
分析：（1）使
+
≤2
成立的正实数a，b满足的条件是a+b=22，利用基本不等式进行证明；
（2）由柯西不等式，求实数m的取值范围．
| a |
| b |
| 11 |
（2）由柯西不等式，求实数m的取值范围．
解答：
解：（1）使
+
≤2
成立的正实数a，b满足的条件是a+b=22
证明：∵2(a+b)=a+b+a+b≥a+b+2
=(
+
)2，
∴
+
≤
=2
；…（5分）
（Ⅱ）由柯西不等式得(1+1+1+1)(a+b+c+d)≥(
+
+
+
)2
即(
+
+
+
)≤
=2
即
≤2，当且仅当a=b=c=d取等号
因不等式
+
+
+
≤m
对任意的正实数a，b，c，d恒成立，
即m≥
对任意的正实数a，b，c，d恒成立，故m≥2．…（10分）
| a |
| b |
| 11 |
证明：∵2(a+b)=a+b+a+b≥a+b+2
| ab |
| a |
| b |
∴
| a |
| b |
| 2(a+b) |
| 11 |
（Ⅱ）由柯西不等式得(1+1+1+1)(a+b+c+d)≥(
| a |
| b |
| c |
| d |
即(
| a |
| b |
| c |
| d |
| (1+1+1+1)(a+b+c+d) |
| a+b+c+d |
即
| ||||||||
|
因不等式
| a |
| b |
| c |
| d |
| a+b+c+d |
即m≥
| ||||||||
|
点评：本题考查基本不等式的运用，考查柯西不等式，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
设l，m，n表示三条不同的直线，α，β表示两个不同的平面，则下列说法正确的是（ ）
| A、若l∥m，m?α，则l∥α |
| B、若l⊥m，l⊥n，m，n?α，则l⊥α |
| C、若l∥α，l∥β，α∩β=m，则l∥m |
| D、若l?α，m?β，l⊥m，则α⊥β |
若一棱锥的底面积是8，则这个棱锥的中截面（过棱锥高的中点且平行于底面的截面）的面积是（ ）
| A、4 | ||
B、2
| ||
| C、2 | ||
D、
|
当x∈（0，5）时，函数y=xlnx的单调性（ ）
| A、是单调增函数 | ||||
| B、是单调减函数 | ||||
C、在（0，
| ||||
D、在（0，
|
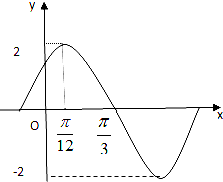已知函数f（x）=Acos（ωx+φ），（A＞0，ω＞0，|φ|＜