题目内容

2．过点$A（\sqrt{3}，1）$的直线${l_1}：\sqrt{3}x+ay-2=0$与过点$B（\sqrt{3}，4）$的直线l2交于点C，若△ABC是以AB为底边的等腰三角形，则l2的方程是$\sqrt{3}$x+y-7=0．

分析 把点A代入直线l1求出a的值，写出l1的方程，
由题意知l1与l2关于直线y=$\frac{5}{2}$对称，
求出点C的坐标，即可写出直线l2的方程．

解答 解：过点$A（\sqrt{3}，1）$的直线${l_1}：\sqrt{3}x+ay-2=0$，
∴$\sqrt{3}$•$\sqrt{3}$+a-2=0，解得a=-1；
∴直线l1的方程为$\sqrt{3}$x-y-2=0；
l1与过点$B（\sqrt{3}，4）$的直线l2交于点C，
且△ABC是以AB为底边的等腰三角形，
如图所示；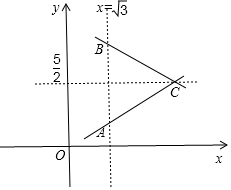
则l1与l2关于直线y=$\frac{5}{2}$对称，
∴点C（$\frac{3\sqrt{3}}{2}$，$\frac{5}{2}$）；
∴直线l2的斜率为k=$\frac{\frac{5}{2}-4}{\frac{3\sqrt{3}}{2}-\sqrt{3}}$=-$\sqrt{3}$，
直线方程为y-4=-$\sqrt{3}$（x-$\sqrt{3}$），
化为一般式：$\sqrt{3}x+y-7=0$．
故答案为：$\sqrt{3}$x+y-7=0．

点评 本题考查了直线方程的应用问题，也考查了数形结合的思想方法，是基础题．

练习册系列答案
相关题目
9．设实数a，b，c分别满足2a3+a=2，blog2b=1，clog5c=1，则a，b，c的大小关系为（　　）
A．a＞b＞cB．b＞a＞cC．c＞b＞aD．a＞c＞b
13．函数x=1在y=2x3-x2+1出的导数值为（　　）
A．3B．2C．5D．4
10．在用二分法求方程零点的算法中，下列说法正确的是（　　）
A．这个算法可以求方程所有的零点
B．这个算法可以求任何方程的零点
C．这个算法能求方程所有的近似零点
D．这个算法并不一定能求方程所有的近似零点
17．设数列{an}的前n项和为Sn，已知a1=1，${a_{n+1}}=\frac{n+2}{n}{S_n}$（n∈N*）．
（1）证明：数列$\left\{{\frac{S_n}{n}}\right\}$是等比数列；
（2）求数列{Sn}的前n项和Tn．
7．已知函数f（x）=2ax+bx-1-2lnx（a∈R）．
（1）当b=0时，讨论函数f（x）的单调区间；
（2）若对?α∈[1，3]，?x∈（0，+∞），f（x）≥2bx-3恒成立，求实数b的取值范围；
（3）当x＞y＞e-1时，求证：exln（y+1）＞eyln（x+1）．
14．下列函数中，为奇函数的是（　　）
A．f（x）=2x-3xB．f（x）=x3+x2C．f（x）=sinxtanxD．$f（x）=lg\frac{1-x}{1+x}$
11．△ABC的三个内角A，B，C的对边分别是a，b，c，则：
①若cosBcosC＞sinBsinC，则△ABC一定是钝角三角形；
②若acosA=bcosB，则△ABC为等腰三角形；
③$\overrightarrow a=（tanA+tanB，tanC）$，$\overrightarrow b=（1，1）$，若$\overrightarrow a•\overrightarrow b＞0$，则△ABC为锐角三角形；
④若O为△ABC的外心，$\overrightarrow{AO}•\overrightarrow{BC}=\frac{1}{2}（{b^2}-{c^2}）$；
⑤若sin2A+sin2B=sin2C，$且\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow 0$，$则\frac{{{{|{\overrightarrow{OA}}|}^2}+{{|{\overrightarrow{OB}}|}^2}}}{{{{|{\overrightarrow{OC}}|}^2}}}=5$
以上叙述正确的序号是①③④⑤．
12．已知$sinα=\frac{4}{5}，α∈（{0，π}）$，则tanα=±$\frac{4}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网