题目内容
6.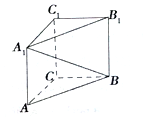 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 由AC∥A1C1,知∠C1A1B是异面直线A1B与AC所成角(或所成角的补角),由此能求出异面直线A1B与AC所成角的余弦值.
解答 解: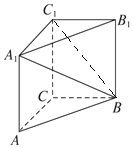 连结BC1,∵AC∥A1C1,
连结BC1,∵AC∥A1C1,
∴∠C1A1B是异面直线A1B与AC所成角(或所成角的补角),
∵在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,
∴AB=$\sqrt{2}$,A1B=$\sqrt{3}$,BC1=$\sqrt{2}$,A1C1=1,
∴cos∠C1A1B=$\frac{1+3-2}{2×1×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴异面直线A1B与AC所成角的余弦值为$\frac{\sqrt{3}}{3}$.
故选:D.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知定义在R上的奇函数f(x)在(0,+∞)上单调递增,f(1)=0,若f(x-2)≥0,则x的取值范围是( )
| A. | [1,3] | B. | [1,2]∪[2,3] | C. | [1,2]∪[3,+∞] | D. | [-∞,1]∪[3,+∞] |