题目内容
12.向量$\overrightarrow{a}$=(sinθ,2m),$\overrightarrow{b}$=(sinθ,cosθ-1),对任意θ∈R,f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$+2<0成立,求实数m的取值范围.分析 利用向量的数量积,求出f(θ),将其转换成含有t的一元二次函数,讨论对称轴的取值,判断其最大值.
解答 解:f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$+2=sin2θ+2m(cosθ-1)+2=-cos2θ+2mcosθ-2m+3,
令cosθ=t,t∈[-1,1]
f(t)=-t2+2mt-2m+3,t∈[-1,1]
对称轴t=m,
当m<1,f(t)[-1,1]单调递减,当t=-1取最大值为-4m+3<0,
∴m>$\frac{3}{4}$,
此时m∈($\frac{3}{4}$,1),
当m≥1,f(t)[-1,1]单调递增,当t=1时取最大值2,不满足,
当0<m<1时,当x=m取最大值,最大值为-(m+1)2+4>0,
m>1或m<-3,不满足,
综上可知,m∈($\frac{3}{4}$,1)时,对任意θ∈R,f(θ)=$\overrightarrow{a}$•$\overrightarrow{b}$+2<0成立.
点评 本题考查向量的数量积及一元二次函数对称轴的取值判断函数的最值,属于中档题.

练习册系列答案
相关题目
3.执行如图所示的程序框图(算法流程图),输出的结果是( )


| A. | 9 | B. | 121 | C. | 130 | D. | 17021 |
20.已知A,B,C是复平面内的三个不同点,点A,B对应的复数分别是-2+3i,-i,若$\overrightarrow{AC}$=$\overrightarrow{CB}$,则点C表示的复数是( )
| A. | -2+2i | B. | -2+4i | C. | -1+i | D. | -1+2i |
17.执行如图所示程序框图,则输出的n为( )


| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
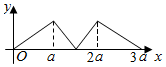
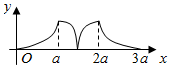
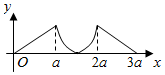
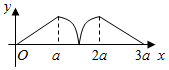
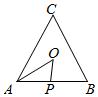 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )