题目内容
2.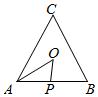 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )| A. | 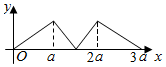 | B. | 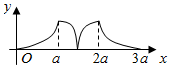 | ||
| C. | 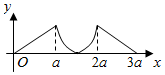 | D. |  |
分析 由三角形的面积公式,结合图象可知需分类讨论求面积,从而利用数形结合的思想方法求得.
解答 解:由三角形的面积公式知,
当0≤x≤a时,
f(x)=$\frac{1}{2}$•x•$\frac{1}{3}$•$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{12}$ax,
故在[0,a]上的图象为线段,
故排除B;
当a<x≤$\frac{3}{2}$a时,
f(x)=$\frac{1}{2}$•($\frac{3}{2}$a-x)•$\frac{2}{3}$•$\frac{\sqrt{3}}{2}$a=$\frac{\sqrt{3}}{6}$a($\frac{3}{2}$a-x),
故在(a,$\frac{3}{2}$a]上的图象为线段,
故排除C,D;
故选A.
点评 本题考查了分类讨论的思想与数形结合的思想应用,同时考查了三角形面积公式的应用.

练习册系列答案
相关题目
15.某辆汽车每次加油都把油箱加满,如表记录了该车相邻两次加油时的情况.
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为8升.
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2015年5月1日 | 12 | 35000 |
| 2015年5月15日 | 48 | 35600 |
在这段时间内,该车每100千米平均耗油量为8升.