题目内容
1．菱形ABCD中，AC长为2，则$\overrightarrow{BA}•\overrightarrow{AC}$=-2．分析 由AC⊥BD可知|AB|×cos∠BAC=$\frac{1}{2}$|AC|=1，利用向量数量积的定义式计算．
解答 
解：设AC中点为O，则|AO|=$\frac{1}{2}$|AC|=1．
∵四边形ABCD是菱形，
∴AC⊥BD．
∴|AB|×cos∠BAC=|AO|=1，
∴$\overrightarrow{BA}•\overrightarrow{AC}$=|AB|×|AC|×cos（180°-∠BAC）=-2|AB|×cos∠BAC=-2×1=-2．
故答案为：2．
点评 本题考查了平面向量的数量积运算，属于基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
9．
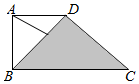如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）
如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）| A． | [-1，1] | B． | $[{-1，\frac{1}{2}}]$ | C． | $[{-\frac{1}{2}，1}]$ | D． | [-1，0] |
16．sin1290°=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | -$\frac{1}{2}$ |