题目内容
20．已知A，B，C是复平面内的三个不同点，点A，B对应的复数分别是-2+3i，-i，若$\overrightarrow{AC}$=$\overrightarrow{CB}$，则点C表示的复数是（ ）| A． | -2+2i | B． | -2+4i | C． | -1+i | D． | -1+2i |
分析 设出C表示的复数，然后利用向量相等，求解即可．
解答 解：设C表示的复数为x+yi，点A，B对应的复数分别是-2+3i，-i，
$\overrightarrow{AC}$=（x+2，y-3），$\overrightarrow{CB}$=（-x，-1-y），
∵$\overrightarrow{AC}$=$\overrightarrow{CB}$，
∴x+2=-x，y-3=-1-y，
解得x=-1，y=1．
点C表示的复数是：-1+i．
故选：C．
点评 本题考查复数的几何意义，复数的坐标表示，考查计算能力．
练习册系列答案
相关题目
9．
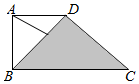如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）
如图，在直角梯形ABCD中，DA=AB=1，BC=2，点P在阴影区域（含边界）中运动，则有$\overrightarrow{AP}•\overrightarrow{BD}$的取值范围是（ ）| A． | [-1，1] | B． | $[{-1，\frac{1}{2}}]$ | C． | $[{-\frac{1}{2}，1}]$ | D． | [-1，0] |