题目内容
已知平面内的向量
,
满足:|
|=2,(
+
)•(
-
)=0,且
⊥
,又
=λ1
+λ2
,0≤λ1≤1,1≤λ2≤2,那么由满足条件的点P所组成的图形的面积是( )
| OA |
| OB |
| OA |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OB |
| A、1 | B、2 | C、4 | D、8 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由条件可得,|
|=|
|=2,不妨以O为原点,以OA方向为x轴正方向,以OB方向为Y轴正方向建立坐标系,则
=(2,0),
=(0,2),求得
=(x,y)=(2λ1,2λ2),可得0<x≤2,2≤y≤4,其表示的平面区域如图,从而求得阴影部分的面积.
| OA |
| OB |
| OA |
| OB |
| OP |
解答:
 解:∵|
解:∵|
|=2,(
+
)•(
-
)=
2-
2=0,∴|
|=|
|=2.
根据
⊥
,不妨以O为原点,以OA方向为x轴正方向,以OB方向为Y轴正方向建立坐标系,
则
=(2,0),
=(0,2),
又
=λ1
+λ2
,0≤λ1≤1,1≤λ2≤2,设
=(x,y),则
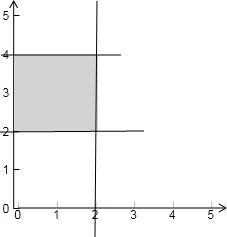
=(2λ1,2λ2),∴0≤x≤2,2≤y≤4,
其表示的平面区域如下图示:
由图可知阴影部分的面积为4,
故选:C.
 解:∵|
解:∵|| OA |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
根据
| OA |
| OB |
则
| OA |
| OB |
又
| OP |
| OA |
| OB |
| OP |
| OP |
其表示的平面区域如下图示:
由图可知阴影部分的面积为4,
故选:C.
点评:本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量坐标形式的运算,关键是正确地画出平面区域,然后结合有关面积公式求解,属于基础题.

练习册系列答案
相关题目
已知λ∈R,函数f(x)=
,g(x)=x2-4x+1+2λ,若关于x的方程f(g(x))=λ有6个解,则λ的取值范围为( )
|
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、(
|
在△ABC中,若(a+b+c)(b+c-a)=2bc,则△ABC是( )
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知偶函数f(x)在[0,+∞)上为单调递减,则满足不等式f(2x-1)>f(3)的x的取值范围是( )
| A、[-1,2] |
| B、[-1,+∞) |
| C、(1,2) |
| D、(-1,2) |
如果偶函数f(x)在区间[1,6]上是增函数且最大值是8,则f(x)在[-6,-1]上是( )
| A、增函数,最大值-8 |
| B、增函数,最小值-8 |
| C、减函数,最大值8 |
| D、减函数,最小值8 |
若与直线3x-y+1=0垂直的直线的倾斜角为α,则cosα的值是( )
| A、3 | ||||
B、-
| ||||
C、
| ||||
D、-
|
设在矩形ABCD中,AB⊥BC,AD⊥DC,若|
|=3,|
|=5,则
•
=( )
| AB |
| AD |
| AC |
| BD |
| A、-16 | B、16 | C、25 | D、15 |
如图是一个空间几何体的三视图,其中正视图和侧视图都是半径为2的半圆,俯视图是半径为2的圆,则该几何体的体积等于( )

A、
| ||
B、
| ||
C、
| ||
D、
|