题目内容
18. 已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.
已知正三棱柱ABC-A1B1C1所有棱长均为2,D、E分别是BC、BB1中点.(1)证明:C1E⊥面ADC1;
(2)求二面角A1-C1D-A的余弦值;
(3)若线段AA1上存在一点P,满足直线CE和直线C1P异面直线成角的余弦值是$\frac{\sqrt{2}}{5}$,求A1P长.
分析 (1)在平面A1B1C1中,过A1作垂直于A1C1的直线为y轴,分别以A1C1、A1A所在直线为x、z轴建立空间直角坐标系,由已知求出所用点的坐标,再由向量数量积为0证明C1E⊥面ADC1内的两条相交直线得答案;
(2)分别求出平面A1C1D与平面AC1D的一个法向量,由两法向量所成角的余弦值可得二面角A1-C1D-A的余弦值;
(3)设P(0,0,m)(m<2),由直线CE和直线C1P异面直线成角的余弦值是$\frac{\sqrt{2}}{5}$列式求得m值即可求得A1P长.
解答 (1)证明:在平面A1B1C1中,过A1作垂直于A1C1的直线为y轴,分别以A1C1、A1A所在直线为x、z轴建立空间直角坐标系,
则C1(2,0,0),C(2,0,2),D($\frac{3}{2},\frac{\sqrt{3}}{2},2$),A(0,0,2),E(1,$\sqrt{3}$,1),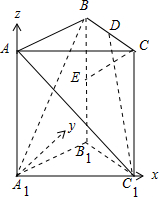
∴$\overrightarrow{CE}=(-1,\sqrt{3},-1)$,$\overrightarrow{AD}=(\frac{3}{2},\frac{\sqrt{3}}{2},0)$,$\overrightarrow{A{C}_{1}}=(2,0,-2)$.
∵$\overrightarrow{CE}•\overrightarrow{A{C}_{1}}=-2+0+2=0$,$\overrightarrow{CE}•\overrightarrow{AD}=-\frac{3}{2}+\frac{3}{2}+0=0$,
∴CE⊥AC1,CE⊥AD,又AD∩AC1=A,
∴C1E⊥面ADC1;
(2)解:设平面A1C1D的一个法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,平面AC1D的一个法向量为$\overrightarrow{{n}_{2}}=({x}_{2},{y}_{2},{z}_{2})$.
由$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{{A}_{1}{C}_{1}}=2{x}_{1}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{{A}_{1}D}=\frac{3}{2}{x}_{1}+\frac{\sqrt{3}}{2}{y}_{1}+2{z}_{1}=0}\end{array}\right.$,取y1=1,得$\overrightarrow{{n}_{1}}=(0,1,-\frac{\sqrt{3}}{4})$.
由$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{A{C}_{1}}=2{x}_{2}-2{z}_{2}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{AD}=\frac{3}{2}{x}_{2}+\frac{\sqrt{3}}{2}{y}_{2}=0}\end{array}\right.$,取z2=1,得$\overrightarrow{{n}_{2}}=(1,-\sqrt{3},1)$.
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{-\frac{5\sqrt{3}}{4}}{\sqrt{5}×\frac{\sqrt{19}}{4}}=-\frac{\sqrt{285}}{19}$.
∴二面角A1-C1D-A的余弦值为$\frac{\sqrt{285}}{19}$;
(3)解:设P(0,0,m)(m<2),
∴$\overrightarrow{{C}_{1}P}=(-2,0,m)$,
由cos<$\overrightarrow{{C}_{1}P},\overrightarrow{CE}$>=$\frac{2-m}{\sqrt{5}•\sqrt{4+{m}^{2}}}=\frac{\sqrt{2}}{5}$,解得m=$\frac{2}{3}$或m=6(舍).
∴A1P长为$\frac{2}{3}$.
点评 本题考查线面垂直的判定,考查空间角的求法,训练了利用空间向量求解空间角,是中档题.

| A. | -5-i | B. | -5+i | C. | 5-i | D. | 5+i |
| A. | $\sqrt{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\sqrt{3}$ |
| A. | 16项 | B. | 17项 | C. | 24项 | D. | 50项 |
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
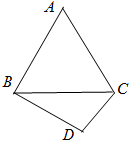 在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.
在△ABC中,角A,B,C的对边分别为a,b,c,满足$\sqrt{3}a=b(sinC+\sqrt{3}cosC)$.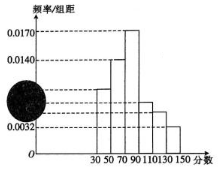 2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.
2017年省内事业单位面向社会公开招聘工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于90分的才有资格参加面试,90分以下(不含90分)则被淘汰.现有2000名竞聘者参加笔试,参加笔试的成绩按区间[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]分段,其频率分布直方图如下图所示(频率分布直方图有污损),但是知道参加面试的人数为500,且笔试成绩在的人数为1440.