题目内容
15.设函数f(x)=$\left\{\begin{array}{l}{{a}^{x},}&{0≤x≤1}\\{\frac{x}{a}+1,}&{-1≤x<0}\end{array}\right.$(a>0且a≠1).若f(x)的最大值与最小值之差为$\frac{3}{2}$,则a的取值为2或$\frac{2}{3}$.分析 对a讨论,分a>1,0<a<1,结合指数函数的单调性,即可得到最值,解方程可得a的值.
解答 解:当a>1时,f(x)在[0,1]递增,
即有f(x)∈[1,a];
f(x)在[-1,0)递增,可得f(x)∈[1-$\frac{1}{a}$,1);
此时f(x)的最大值为a,最小值为1-$\frac{1}{a}$,
由a-(1-$\frac{1}{a}$)=$\frac{3}{2}$,解得a=2($\frac{1}{2}$舍去);
当0<a<1时,f(x)在[0,1]递减,
即有f(x)∈[a,1];
f(x)在[-1,0)递增,可得f(x)∈[1-$\frac{1}{a}$,1);
此时f(x)的最大值为1,最小值为1-$\frac{1}{a}$,
由1-(1-$\frac{1}{a}$)=$\frac{3}{2}$,解得a=$\frac{2}{3}$.
综上可得a=2或$\frac{2}{3}$.
故答案为:2或$\frac{2}{3}$.
点评 本题考查函数的最值的求法,注意运用分类讨论的思想方法,结合指数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.过圆x2+y2=4上一点($\sqrt{2}$,1)的切线方程为( )
| A. | x+$\sqrt{2}$y=4 | B. | $\sqrt{2}$x+y=3 | C. | $\sqrt{2}$x+y=4 | D. | x+$\sqrt{2}$y=2 |
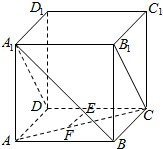 如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.
如图,正方体ABCD-A1B1C1D1中,E是A1B上的点,F是AC上的点,且A1E=2EB,CF=2AF.求证:EF∥平面A1B1CD.