题目内容
4.求适合下列条件的抛物线的标准方程:(1)过点M(-6,6);
(2)焦点F在直线l:3x-2y-6=0上.
分析 (1)根据题意,分析可得要求抛物线开口向左或开口向上,进而分情况求出抛物线的方程,综合可得答案;
(2)根据题意,求出直线与坐标轴交点坐标,进而可得抛物线焦点的坐标,分别求出抛物线的方程,综合可得答案.
解答 解:(1)抛物线过点M(-6,6),则其开口向左或开口向上,
若其开口向左,设其方程为y2=-2px,
将M(-6,6)代入方程可得:62=-2p×(-6),
解可得,p=3,
此时其标准方程为:y2=-6x,
若其开口向上,设其方程为x2=2py,
将M(-6,6)代入方程可得:(-6)2=2p×6,
解可得,p=3,
此时其标准方程为:x2=6y,
综合可得:抛物线的方程为:y2=-6x或x2=6y;
(2)根据题意,直线l:3x-2y-6=0与坐标轴交点为(2,0)和(0,-3);
则要求抛物线的焦点为(2,0)或(0,-3),
若其焦点为(2,0),则其方程为y2=4x,
若其焦点为(0,-3),则其方程为x2=-6y,
综合可得:抛物线的方程为:y2=4x或x2=-6y.
点评 本题考查抛物线的标准方程求法,注意要先确定抛物线焦点的位置,如不能确定,需要分情况讨论.

练习册系列答案
相关题目
9.若函数y=f(x)在区间(a,b)内可导,且x0∈(a,b)则$\lim_{h→0}\frac{{f({x_0}-h)\;-f({x_0})}}{h}$的值为( )
| A. | f′(x0) | B. | -f′(x0) | C. | -2f′(x0) | D. | 0 |
14.ω是正实数,函数f(x)=2cosωx在x∈$[{0,\frac{2π}{3}}]$上是减函数,且有最小值1,那么ω的值可以是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 3 |
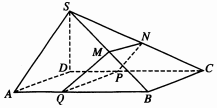 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥平面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC的中点,过MN作平面MNPQ分别与线段CD,AB相交于P,Q两点(不与A,B重合).