题目内容

9．若函数y=f（x）在区间（a，b）内可导，且x0∈（a，b）则$\lim_{h→0}\frac{{f（{x_0}-h）\;-f（{x_0}）}}{h}$的值为（　　）
A．f′（x0）B．-f′（x0）C．-2f′（x0）D．0

分析 将已知的等式变形为符合导数定义的形式，利用导数定义得到答案．

解答 解：$\lim_{h→0}\frac{{f（{x_0}-h）\;-f（{x_0}）}}{h}$=$\underset{lim}{n→∞}\frac{f（{x}_{0}-h）-f（{x}_{0}）}{-h}×（-1）$=-f'（x0）；
故选B．

点评 本题考查了导数的定义；正确将已知等式变形为符合导数定义的形式是关键．

练习册系列答案
相关题目
16．记U={1，2，…，100}，对数列{an}（n∈N*）和U的子集T，若T=∅，定义ST=0；若T={t1，t2，…，tk}，定义ST=a${\;}_{{t}_{1}}$+a${\;}_{{t}_{2}}$+…+a${\;}_{{t}_{k}}$．例如：T={1，3，66}时，ST=a1+a3+a66．现设{an}（n∈N*）是公比为3的等比数列，且当T={2，4}时，ST=30．
（1）求数列{an}的通项公式；
（2）对任意正整数k（1≤k≤100），若T⊆{1，2，…，k}，求证：ST＜ak+1；
（3）对任意正整数k（1≤k≤100），若T={1，2，…，k}，记数列{$\frac{1}{{S}_{T}}$}的前k项和为H，求证：H＜$\frac{3}{2}$．
20．三角形ABC中sinA=$\frac{4}{5}$，cosB=$\frac{5}{13}$，c=56，求sinC及三角形ABC外接圆的周长．
17．设数列{an}的前n项和为Sn，已知a1=1，${a_{n+1}}=\frac{n+2}{n}{S_n}$（n∈N*）．
（1）证明：数列$\left\{{\frac{S_n}{n}}\right\}$是等比数列；
（2）求数列{Sn}的前n项和Tn．
4．求适合下列条件的抛物线的标准方程：
（1）过点M（-6，6）；
（2）焦点F在直线l：3x-2y-6=0上．
14．下列函数中，为奇函数的是（　　）
A．f（x）=2x-3xB．f（x）=x3+x2C．f（x）=sinxtanxD．$f（x）=lg\frac{1-x}{1+x}$
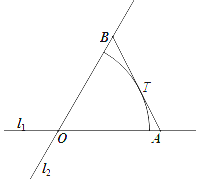1．若$\overrightarrow{a}$与$\overrightarrow{b}$是非零向量，且|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$的方向与$\overrightarrow{a}$+$\overrightarrow{b}$的方向所成的角是（　　）
A．0°B．60°C．30°D．45°
18．如图，在某商业区周边有两条公路l1和l2，在点O处交汇；该商业区为圆心角$\frac{π}{3}$、半径3km的扇形．现规划在该商业区外修建一条公路AB，与l1，l2分别交于A，B，要求AB与扇形弧相切，切点T不在l1，l2上．
（1）设OA=akm，OB=bkm试用a，b表示新建公路AB的长度，求出a，b满足的关系式，并写出a，b的范围；
（2）设∠AOT=α，试用α表示新建公路AB的长度，并且确定A，B的位置，使得新建公路AB的长度最短．
19．若直线a2x+y+7=0和直线x-2ay+1=0垂直，则实数a的值为0或2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网