题目内容
13.已知M(3,-2),N(-5,-1),且$\overrightarrow{MP}=\frac{1}{3}\overrightarrow{MN}$,则P点的坐标是($\frac{1}{3}$,-$\frac{5}{3}$).分析 设出点P的坐标,利用平面向量的坐标运算与向量相等列出方程组,求出x、y的值即可.
解答 解:设点P(x,y),由M(3,-2),N(-5,-1),
∴$\overrightarrow{MP}$=(x-3,y+2),
$\overrightarrow{MN}$=(-8,1),
又$\overrightarrow{MP}=\frac{1}{3}\overrightarrow{MN}$,
∴$\left\{\begin{array}{l}{x-3=-\frac{8}{3}}\\{y+2=\frac{1}{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=-\frac{5}{3}}\end{array}\right.$;
∴P点的坐标是($\frac{1}{3}$,-$\frac{5}{3}$).
故答案为:($\frac{1}{3}$,-$\frac{5}{3}$).
点评 本题考查了平面向量的坐标表示与线性运算问题,是基础题.

练习册系列答案
相关题目
5.如图是一个几何体的三视图,则该几何体的体积为( )


| A. | 16 | B. | $4\sqrt{2}$ | C. | 48 | D. | 32 |
2. 某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.
某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“上网迷“与性别有关?
(2)将上述调查所得到的频率视为概率.现在从该地区大量高三学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名学生中的“上网迷”人数为X.若每次抽取的结果是相互独立的,求X=2的概率.
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{({n}_{11}+{n}_{12})({n}_{21}+{n}_{22})({n}_{11}+{n}_{21})({n}_{12}+{n}_{22})}$,
.
 某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.
某教育机构为了解本地区高三学生上网的情况,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天上网时间的频率分布直方图:将每天上网时间不低于40分钟的学生称为“上网迷”.(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“上网迷“与性别有关?
| 非上网迷 | 上网迷 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{({n}_{11}+{n}_{12})({n}_{21}+{n}_{22})({n}_{11}+{n}_{21})({n}_{12}+{n}_{22})}$,
| P(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
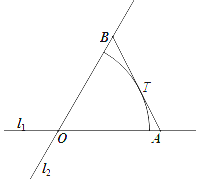 如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.
如图,在某商业区周边有两条公路l1和l2,在点O处交汇;该商业区为圆心角$\frac{π}{3}$、半径3km的扇形.现规划在该商业区外修建一条公路AB,与l1,l2分别交于A,B,要求AB与扇形弧相切,切点T不在l1,l2上.