Question

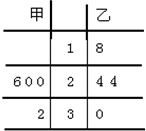甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如图所示：
（1）求乙球员得分的平均数和方差；
（2）求甲乙在一场比赛里得分的和的分布列和期望．

Answer 1

考点：离散型随机变量的期望与方差,离散型随机变量及其分布列

专题：概率与统计

分析：（Ⅰ）由茎叶图知，乙球员四场比赛得分为18，24，24，30，由此能求出乙球员得分的平均数和方差．（Ⅱ）甲球员四场比赛得分为20，20，26，32，分别从两人得分中随机选取一场的得分，共有4×4=16种情况，得分和Y的结果有38，44，50，56，62，由此能求出甲乙在一场比赛里得分的和的分布列和期望．

解答： 解：（Ⅰ）由茎叶图知，乙球员四场比赛得分为18，24，24，30，
平均数

.

x

=

1

4

（18+24+24+30）=24．
S²=

1

4

[（18-24）²+（24-24）²+（24-24）²+（30-24）²]=18．
（Ⅱ）甲球员四场比赛得分为20，20，26，32，
分别从两人得分中随机选取一场的得分，共有4×4=16种情况，
得分和Y的结果有38，44，50，56，62，
P（Y=38）=

1

8

，P（Y=44）=

5

16

，
P（Y=50）=

5

16

，P（Y=56）=

3

16

，
P（Y=62）=

1

16

，
得分和Y的分布列为：

Y	38	44	50	56	62
P	1 8	5 16	5 16	3 16	1 16

…11分
数学期望EY=38×

1

8

+44×

5

16

+50×

3

16

+62×

1

16

=48.5．

点评：本题考查平均数和方差的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．