题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x-c,0<x≤1}\\{{x}^{2}-bx-1,x>1}\end{array}\right.$在(0,+∞)上不是单调函数,设b、c为常数(1)若c=0,求b的取值范围;
(2)若b≤2,c>1,且f(c)-f(b)≠k(c2-b2),求k的取值范围.
分析 (1)c=0时,得出$f(x)=\left\{\begin{array}{l}{lo{g}_{2}x}&{0<x≤1}\\{{x}^{2}-bx-1}&{x>1}\end{array}\right.$,而f(x)在(0,+∞)上不是单调函数,从而根据二次函数和分段函数的单调性得到$\frac{b}{2}>1$,或$\left\{\begin{array}{l}{\frac{b}{2}≤1}\\{{1}^{2}-b•1-1<lo{g}_{2}1}\end{array}\right.$,这样便可求出b的取值范围;
(2)可判断出f(x)在(1,+∞)上为增函数,从而要使f(x)在(0,+∞)上不是单调函数,便可得出b>c,从而求出f(c)-f(b)=c2-bc,这便得到$k≠\frac{c}{c+b}$,而可求得$\frac{c}{c+b}<\frac{1}{2}$,从而便有$k≥\frac{1}{2}$,这便得出了k的取值范围.
解答 解:(1)c=0时,$f(x)=\left\{\begin{array}{l}{lo{g}_{2}x}&{0<x≤1}\\{{x}^{2}-bx-1}&{x>1}\end{array}\right.$;
∵f(x)在(0,+∞)上不是单调函数;
∴$\frac{b}{2}>1$,或$\left\{\begin{array}{l}{\frac{b}{2}≤1}\\{{1}^{2}-b•1-1<lo{g}_{2}1}\end{array}\right.$;
∴b>2,或0<b≤2;
∴b的取值范围为(0,+∞);
(2)b≤2;
∴$\frac{b}{2}≤1$;
∴f(x)在(1,+∞)上为增函数;
∴要使f(x)在(0,+∞)上不是单调函数,则:12-b•1-1<log21-c;
∴-b<-c;
∴b>c;
又c>1,∴b>1;
∴f(c)-f(b)=c2-bc-1-(b2-b2-1)=c2-bc;
∴c2-bc≠k(c2-b2);
∴$k≠\frac{{c}^{2}-bc}{{c}^{2}-{b}^{2}}=\frac{c}{c+b}$;
∵b>c>1;
∴b+c>2c;
∴$\frac{c}{c+b}<\frac{1}{2}$;
∴$k≥\frac{1}{2}$;
∴k的取值范围为$[\frac{1}{2},+∞)$.
点评 考查对数函数的单调性,以及二次函数和分段函数单调性的判断,已知函数求值的方法,不等式的性质.

(1)甲、乙两人都不入选.
(2)甲、乙两人至多1人入选.
(3)甲、乙、丙3人至少有1人入选.
(4)甲、乙、丙3人至多有2人入选.
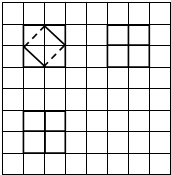 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 6 | B. | $\frac{20}{3}$ | C. | 7 | D. | $\frac{22}{3}$ |
| A. | $\frac{5}{9}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |