题目内容
16．
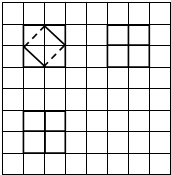如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体的体积为（ ）| A． | 6 | B． | $\frac{20}{3}$ | C． | 7 | D． | $\frac{22}{3}$ |
分析 根据三视图可知几何体是一个棱长为2的正方体，分别在A、B、C、D四个角上截取一个直三棱柱，再由条件和主体的体积公式求出答案．
解答 
解：根据三视图可知几何体是一个棱长为2的正方体，
分别在A、B、C、D四个角上截取一个直三棱柱，底面是直角边分别是1、1的等腰直角三角形，且高为1，
所以几何体的体积V=2×2×2-4×$\frac{1}{2}×1×1×1$=6，
故选：A．
点评 本题考查三视图求几何体的体积，考查空间想象能力，三视图正确复原几何体是解题的关键，属于中档题．
练习册系列答案
相关题目
11．
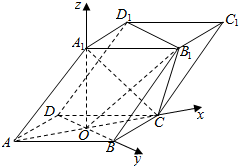如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=$\sqrt{2}$．平面OCB1的法向量$\overrightarrow{n}$=（x，y，z）为（ ）
如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=$\sqrt{2}$．平面OCB1的法向量$\overrightarrow{n}$=（x，y，z）为（ ）| A． | （0，1，1） | B． | （1，-1，1） | C． | （0，1，-1） | D． | （-1，-1，1） |
如图，四棱锥P-ABCD中，底面ABCD是正方形，PA是四棱锥P-ABCD的高，PA=AB=2，点M，N，E分别是PD，AD，CD的中点．
8．在定义域内既是奇函数又是减函数的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=-x+$\frac{1}{x}$ | ||
| C． | y=-x|x| | D． | y=$\left\{\begin{array}{l}{-x+1，x＞0}\\{-x-1，x≤0}\end{array}\right.$ |
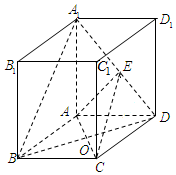如图，四棱柱ABCD-A1B1C1D1中，底面四边形ABCD为菱形，∠ABC=60°，AA1=AC=2，A1B=A1D=2$\sqrt{2}$，点E在线段A1D上．