题目内容
14.已知函数f(x)=$\left\{{\begin{array}{l}{{2^x}-\frac{a}{3},x≤0}\\{lnx-2x+a,x>0}\end{array}}$有三个不同的零点,则实数a的取值范围是( )| A. | (1+ln2,3] | B. | (ln2,3] | C. | (0,1+ln2) | D. | (0,3] |
分析 求出当x>0时的函数的导数,研究函数的极值,利用分段函数的性质进行判断求解即可.
解答  解:当x>0时,函数f(x)=lnx-2x+a,此时函数的导数f′(x)=$\frac{1}{x}$-2=$\frac{1-2x}{x}$,
解:当x>0时,函数f(x)=lnx-2x+a,此时函数的导数f′(x)=$\frac{1}{x}$-2=$\frac{1-2x}{x}$,
由f′(x)>0得0<x<$\frac{1}{2}$,此时函数递增,
由f′(x)<0得x>$\frac{1}{2}$,此时函数递减,
即当x=$\frac{1}{2}$时,函数取得极大值,f($\frac{1}{2}$)=ln$\frac{1}{2}$-1+a=-1-ln2+a,
当x→0时,f(x)=lnx-2x+a→-∞,
当x≤0时,函数f(x)=2x-$\frac{a}{3}$为增函数,且此时-$\frac{a}{3}$<f(x)≤1-$\frac{a}{3}$,
要使函数f(x)有三个不同的零点,
则满足$\left\{\begin{array}{l}{-\frac{a}{3}<0}\\{1-\frac{a}{3}≥0}\\{-1-ln2+a>0}\end{array}\right.$,即$\left\{\begin{array}{l}{a>0}\\{a≤3}\\{a>1+ln2}\end{array}\right.$,
即1+ln2<a≤3,
即实数a的取值范围是(1+ln2,3],
故选:A.
点评 本题考查根的存在性及根的个数的判断,数形结合以及求函数的导数判断函数的极值是解决问题的关键,属中档题

练习册系列答案
相关题目
7.圆C经过直线x+y-1=0与x2+y2=4的交点,且圆C的圆心为(-2,-2),则过点(2,4)向圆C作切线,所得切线方程为( )
| A. | 5x-12y+38=0 | B. | 5x+12y+38=0 | ||
| C. | 5x-12y+38=0或x=2 | D. | 5x+12y+38=0或x=4 |
2.某几何体的三视图如图所示,其则该几何体的体积是( )
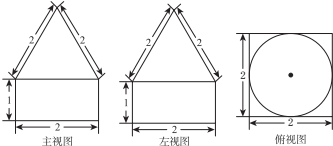

| A. | $2+\frac{{\sqrt{3}}}{3}π$ | B. | $4+\sqrt{3}π$ | C. | $\frac{4}{3}+\frac{{\sqrt{3}}}{3}π$ | D. | $4+\frac{{\sqrt{3}}}{3}π$ |
 如图,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$.
如图,在直三棱柱ADF-BCE中,AB=BC=BE=2,CE=$2\sqrt{2}$. 某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).