题目内容
6.已知正数a,b满足a+b=1.(1)求ab的取值范围;
(2)求ab+$\frac{1}{ab}$的最小值.
分析 (1)利用基本不等式的性质即可得出.
(2)令ab=x∈$(0,\frac{1}{4}]$.f(x)=x+$\frac{1}{x}$,利用导数研究其单调性即可得出.
解答 解:(1)∵正数a,b满足a+b=1,∴1$≥2\sqrt{ab}$,解得ab$≤\frac{1}{4}$,当且仅当a=b=$\frac{1}{2}$时取等号,
∴ab∈$(0,\frac{1}{4}]$.
(2)令ab=x∈$(0,\frac{1}{4}]$.f(x)=x+$\frac{1}{x}$,f′(x)=1-$\frac{1}{{x}^{2}}$<0,因此函数f(x)在x∈$(0,\frac{1}{4}]$单调递减,
∴f(x)≥$f(\frac{1}{4})$=$\frac{17}{4}$.
∴当且仅当ab=$\frac{1}{4}$时,ab+$\frac{1}{ab}$取得最小值$\frac{17}{4}$.
点评 本题考查了基本不等式的性质、利用导数研究其单调性极值与最值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)=$\left\{{\begin{array}{l}{{2^x}-\frac{a}{3},x≤0}\\{lnx-2x+a,x>0}\end{array}}$有三个不同的零点,则实数a的取值范围是( )
| A. | (1+ln2,3] | B. | (ln2,3] | C. | (0,1+ln2) | D. | (0,3] |
18.在同一坐标系中,函数y=sinx,x∈[0,2π]与y=sinx,x∈[2π,4π]的图象( )
| A. | 重合 | B. | 形状相同,位置不同 | ||
| C. | 关于y轴对称 | D. | 形状不同,位置不同 |
16.若正数a,b满足ab-(a+b)=1,则a+b的最小值是( )
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
 ,
,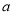 是
是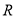 上的常数,若
上的常数,若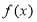 的值域为
的值域为 ,则
,则 取值范围为( )
取值范围为( )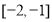 B.
B.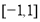
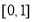 D.
D.