题目内容
4.命题p:“?x0∈R“,x02-1≤0的否定¬p为( )| A. | ?x∈R,x2-1≤0 | B. | ?x∈R,x2-1>0 | C. | ?x0∈R,x02-1>0 | D. | ?x0∈R,x02-1<0 |
分析 直接写出特称命题的否定得答案.
解答 解:命题p:“?x0∈R“,x0-1≤0为特称命题,其否定为全称命题,
∴¬p为?x∈R,x2-1>0.
故选:B.
点评 本题考查特称命题的否定,注意命题的否定的格式是关键,是基础题.

练习册系列答案
相关题目
15.某空间几何体的三视图如图所示,其中俯视图是半径为1的圆,则该几何体的体积是( )
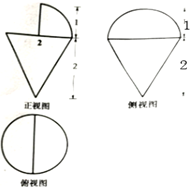

| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
12.已知$cos({α-\frac{π}{6}})+sinα=\frac{{4\sqrt{3}}}{5}$,且$α∈({\frac{π}{2},π})$,则$sin({α+\frac{π}{3}})$的值是( )
| A. | $\frac{{4\sqrt{3}-3}}{10}$ | B. | $\frac{{4\sqrt{3}+3}}{10}$ | C. | $\frac{{3\sqrt{3}-4}}{10}$ | D. | $\frac{{3\sqrt{3}+4}}{10}$ |
9.双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为( )
| A. | y=±3x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
16.若变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y-3≤0}\\{y≥1}\end{array}\right.$,则目标函数z=-2x+y的最大值为( )
| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | -3 |
9.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P在C的渐进线上,PF1⊥x轴,若△PF1F2为等腰直角三角形,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$ |