题目内容
9.双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为( )| A. | y=±3x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
分析 将双曲线的方程的右边的“1”换为“0”可得双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为$\frac{{x}^{2}}{3}$-y2=0,整理后就得到双曲线的渐近线方程.
解答 解:∵双曲线的方程为$\frac{{x}^{2}}{3}$-y2=1,
∴将右边的“1”换为“0”可得:
双曲线$\frac{{x}^{2}}{3}$-y2=1的渐近线方程为$\frac{{x}^{2}}{3}$-y2=0,即y=±$\frac{\sqrt{3}}{3}$x.
故选:D.
点评 本题考查双曲线的标准方程,以及双曲线的简单性质的应用,令标准方程中的“1”为“0”即可求出渐近线方程.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
19.在区间[-3,3]内随机取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
4.命题p:“?x0∈R“,x02-1≤0的否定¬p为( )
| A. | ?x∈R,x2-1≤0 | B. | ?x∈R,x2-1>0 | C. | ?x0∈R,x02-1>0 | D. | ?x0∈R,x02-1<0 |
14.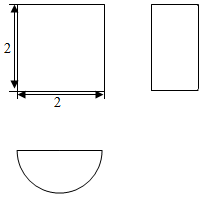 已知一个几何体的三视图如图所示,其中俯视图为半圆面,则该几何体的体积为( )
已知一个几何体的三视图如图所示,其中俯视图为半圆面,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,其中俯视图为半圆面,则该几何体的体积为( )
已知一个几何体的三视图如图所示,其中俯视图为半圆面,则该几何体的体积为( )| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{3}$ |
1.平行于直线l:x+2y-3=0,且与l的距离为2$\sqrt{5}$的直线的方程为( )
| A. | x+2y+7=0 | B. | x+2y-13=0或x+2y+7=0 | ||
| C. | x+2y+13=0 | D. | x+2y+13=0或x+2y-7=0 |
13.已知复数z=a+(a-2)i(a∈R,i是虚数单位)为实数,则$\int_0^a{\sqrt{4-{x^2}}dx}$的值是( )
| A. | 2+π | B. | $2+\frac{π}{2}$ | C. | π | D. | 4+4π |
14.设F为抛物线C:y2=8x,曲线y=$\frac{k}{x}$(k>0)与C交于点A,直线FA恰与曲线y=$\frac{k}{x}$(k>0)相切于点A,直线FA于C的准线交于点B,则$\frac{|FA|}{|BA|}$等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |