题目内容
函数y=
（x＜0）的值域是（ ）
| 3x |
| x2+x+1 |
| A、（-1，0） |
| B、[-3，0） |
| C、[-3，-1] |
| D、（-∞，0） |
考点：函数的值域
专题：计算题,函数的性质及应用
分析：函数即为y=
，运用基本不等式，求得x+
≤-2，即可得到函数y的值域．
| 3 | ||
x+
|
| 1 |
| x |
解答：
解：函数y=
（x＜0）
即为y=
，
由于x＜0，则x+
=-[（-x）+
]≤-2，
则有x+
+1≤-1，
则有y≥-3，且y＜0，
则有函数的值域为[-3，0）．
故选B．
| 3x |
| x2+x+1 |
即为y=
| 3 | ||
x+
|
由于x＜0，则x+
| 1 |
| x |
| 1 |
| -x |
则有x+
| 1 |
| x |
则有y≥-3，且y＜0，
则有函数的值域为[-3，0）．
故选B．
点评：本题考查函数的值域的求法，考查基本不等式的运用：求最值，考查运算能力，属于中档题．
练习册系列答案
相关题目
若直线AB的斜率是
，将直线AB绕A点按逆时针方向旋转45°后，所得直线的倾斜角是（ ）
| 3 |
| A、105° | B、15° |
| C、75° | D、120° |
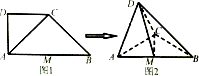如图1，在四边形ABCD中，AD⊥CD，CD∥AB，AB=2AD=2CD=4，M为线段AB的中点，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D-ABC，如图2，所示．
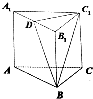如图，在直三棱柱ABC-A1B1C1中，AC=BC=CC1=2，∠ACB=90°，D是AA1的中点．