题目内容
7.观察($\frac{1}{x}$)'=-$\frac{1}{x^2}$,(x3)'=3x2,(sinx)'=cosx,由归纳推理可得:若函数f(x)在其定义域上满足f(-x)=-f(x),记g(x)为f(x)的导函数,则g(-x)=( )| A. | -f(x) | B. | f(x) | C. | g(x) | D. | -g(x) |
分析 由已知中($\frac{1}{x}$)'=-$\frac{1}{x^2}$,(x3)'=3x2,(sinx)'=cosx,…分析其规律,我们可以归纳推断出,奇函数的导数是偶函数,即可得到答案.
解答 解:由给出的例子可以归纳推理得出“奇函数的导数是偶函数”,
∵若函数f(x)在其定义域上满足f(-x)=-f(x),
∴f(x)为奇函数,
∵g(x)为f(x)的导函数,
∴g(-x)=g(x).
故选:C
点评 本题考查的知识点是归纳推理,及函数奇偶性的性质,其中根据已知中原函数与导函数奇偶性的关系,得到结论是解答本题的关键.

练习册系列答案
相关题目
17.某几何体的三视图如图所示,则该几何体的表面积为( )
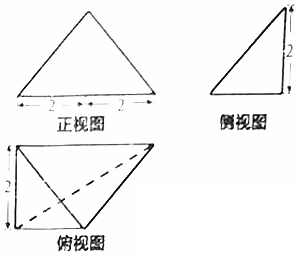

| A. | $6+4\sqrt{2}+2\sqrt{6}$ | B. | $4+6\sqrt{2}+2\sqrt{5}$ | C. | $4+2\sqrt{5}+2\sqrt{6}$ | D. | $4+6\sqrt{2}+2\sqrt{6}$ |
15.执行如图所示的程序框图,输出的S值为( )
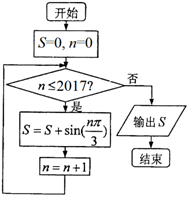

| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
 一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.
一个均速旋转的摩天轮每12分钟逆时针旋转一周,最低点距地面2米,最高点距地面18米,甲从摩天轮最低点处上摩天轮,3分钟后乙也在其最低点处上摩天轮,从乙上摩天轮开始计时,在摩天轮转动的一圈内,有3分钟,甲、乙距地面的高度之和不小于28米.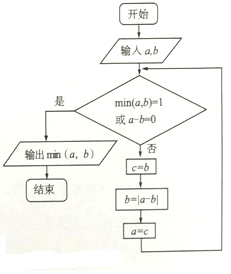 min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )
min(a,b)表示a,b中的最小值,执行如图所示的程序框图,若输入的a,b值分别为4,10,则输出的min(a,b)值是( )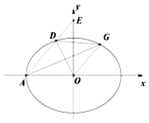 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.