题目内容
掷一枚均匀的硬币3次,出现正面的次数多于反面的次数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:计算题,概率与统计
分析:求出出现2次正面一次反面的概率,再加上3次都是正面的概率,即为所求.
解答:
解:将一枚均匀的硬币投掷3次,出现2次正面一次反面的概率等于
•(
)2•
=
.
3次都是正面的概率等于(
)3=
,
∴掷一枚均匀的硬币3次,出现正面的次数多于反面的次数的概率是
+
=
.
故选:B.
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
3次都是正面的概率等于(
| 1 |
| 2 |
| 1 |
| 8 |
∴掷一枚均匀的硬币3次,出现正面的次数多于反面的次数的概率是
| 3 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
故选:B.
点评:本题考查n次独立重复试验中恰好发生k次的概率,考查互斥事件的概率,是一个基础题,解题的关键是看清题目所给的条件符合什么规律,在按照规律解题,体现了分类讨论的数学思想.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
当a取下列哪个值时,函数f (x)=2x3-9x2+12x-a恰好有两个不同的零点( )
| A、8 | B、6 | C、4 | D、2 |
下列各函数中,是偶函数且在区间(0,π)上为增函数的是( )
| A、y=cosx |
| B、y=sinx |
| C、y=-cosx |
| D、y=-cos2x |
函数y=log
(cosx)的一个单调减区间为( )
| 1 |
| 2 |
| A、(-π,0) | ||
| B、(0,π) | ||
C、(0,
| ||
D、(-
|
设复数z满足iz=1+2i,则z=( )
| A、2-i | B、-2-i |
| C、-2+i | D、2+i |
已知lg(x+y)+lg(2x+3y)-lg3=lg4+lgx+lgy,则
的值( )
| x |
| y |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、3或0 |
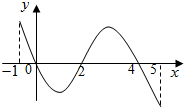 已知函数f(x)的定义域为[-1,5],部分对应值如下表:
已知函数f(x)的定义域为[-1,5],部分对应值如下表: 某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.
某产品的组装工序图如图,图中各字母表示不同车间,箭头上的数字表示组装过程中该工序所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工序,组装该产品需要流经所有工序,则组装该产品所需要的最短时间是( )小时.