题目内容
已知等差数列{an},an=4n-3,则首项a1为 ,公差d为 .
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:根据等差数列的通项公式求出公差d,令n=1求得首项a1.
解答:
解:由题意得,等差数列{an},an=4n-3,
则公差d=4,令n=1得首项a1=1,
故答案为:1、4.
则公差d=4,令n=1得首项a1=1,
故答案为:1、4.
点评:本题考查等差数列的通项公式,n的系数是公差,属于基础题.

练习册系列答案
相关题目
已知函数f(x)在区间[-5,5]上是奇函数,在区间[0,5]上是单调函数,且f(3)<f(1),则( )
| A、f(-1)<f(-3) |
| B、f(0)>f(-1) |
| C、f(-1)<f(1) |
| D、f(-3)>f(-5) |
要得到函数y=cosx的图象,只需把函数y=sin2x的图象( )
A、沿x轴向左平移
| ||||
B、沿x轴向右平移
| ||||
C、横坐标缩短为原来的
| ||||
D、横坐标伸长为原来的2倍,纵坐标不变,再沿x轴向左平移
|
若f(x)=ax2-
,a为一个正常数,且f(f(
))=-
,那么a的值为( )
| 2 |
| 2 |
| 2 |
A、
| ||||
B、2-
| ||||
C、
| ||||
D、
|
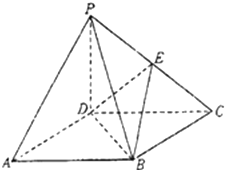 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.