题目内容
已知关于x的方程cos2x-sin2x-2sinx+2a+1=0在区间(0,
]内有解,则实数a的取值范围是( )
| π |
| 2 |
| A、(-1.1] |
| B、(-1,1) |
| C、[0,1) |
| D、[-1,0) |
考点:三角函数的最值
专题:计算题,三角函数的图像与性质,不等式的解法及应用
分析:由于x∈(0,
],则0<t=sinx≤1.由题意可得方程t2+t-a-1=0 在(0,1]上有解,函数f(t)=t2+t的对称轴为t=-
,可得f(t)的值域,由0<a+1≤2,即可得到a的范围.
| π |
| 2 |
| 1 |
| 2 |
解答:
解:方程cos2x-sin2x-2sinx+2a+1=0,
即-2sin2x-2sinx+2a+2=0.
由于x∈(0,
],∴0<t=sinx≤1.
故方程-t2-t+a+1=0 在(0,1]上有解.
即为a+1=t2+t在(0,1]上有解.
二次函数f(t)=t2+t的对称轴为t=-
∉(0,1],
(0,1]为增区间,则f(t)∈(0,2],
由0<a+1≤2,
解得-1<a≤1.
故选:A.
即-2sin2x-2sinx+2a+2=0.
由于x∈(0,
| π |
| 2 |
故方程-t2-t+a+1=0 在(0,1]上有解.
即为a+1=t2+t在(0,1]上有解.
二次函数f(t)=t2+t的对称轴为t=-
| 1 |
| 2 |
(0,1]为增区间,则f(t)∈(0,2],
由0<a+1≤2,
解得-1<a≤1.
故选:A.
点评:本题主要考查同角三角函数的基本关系,考查二次函数在闭区间上的最值问题,体现了转化的数学思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
在某市举办的城市运动会的跳高比赛中,甲、乙两名跳高运动员一次试跳2米高度成功的概率分别是0.7、0.6,且每次试跳成功与否相互之间没有影响,若甲、乙各试跳两次,则两人中恰有一人第二次才成功的概率为 .
若k∈[-3,3],则k的值使得过A(1,1)可以做两条直线与圆(x-k)2+y2=2相切的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
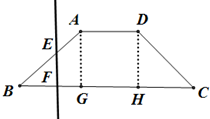 如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2
如图,已知底角为45°的等腰梯形ABCD,底边BC长为5cm,腰长为2