题目内容
15. 已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.
已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.(Ⅰ)求椭圆C的方程;
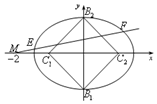
(Ⅱ)设M(2,0),过点M的直线与椭圆C相交于E,F两点,当线段EF的中点落在由四点C1(-1,0),C2(1,0),B1(0,-1),B2(0,1)构成的四边形内(包括边界)时,求直线斜率的取值范围.
分析 (Ⅰ)设右焦点为(c,0),过右焦点斜率为l的直线方程为:y=x-c,则原点到直线的距离可得c=1,a=$\sqrt{2}$,得到椭圆方程.
(Ⅱ)显然直线的斜率k存在,所以可设直线的方程为y=k(x+2),设点E,F的坐标分别为(x1,y1),(x2,y2),线段EF的中点为G(x0,y0),联立直线与椭圆方程,利用判别式以及韦达定理,通过点G在正方形内(包括边界)的充要条件为$\left\{\begin{array}{l}{{y}_{0}≤{x}_{0}+1}\\{{y}_{0}≥-{x}_{0}-1}\end{array}\right.$ 求解k的范围即可.
解答 解:(Ⅰ)设右焦点为(c,0),
则过右焦点斜率为l的直线方程为:y=x-c …(1分)
则原点到直线的距离d=$\frac{|c|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ 得c=1,a=$\sqrt{2}$ …(3分)
所以$\frac{{x}^{2}}{2}+{y}^{2}=1$ …(4分)
(Ⅱ)显然直线的斜率k存在,所以可设直线的方程为y=k(x+2),
设点E,F的坐标分别为(x1,y1),(x2,y2),
线段EF的中点为G(x0,y0),
由$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(1+2k2)x2+8k2x+8k2-2=0
由△=(8k2)-4(1+2k2)(8k2-2)>0解得$-\frac{\sqrt{2}}{2}<k<\frac{\sqrt{2}}{2}$ …(1)…(7分)
由韦达定理得x1+x2=$\frac{-8{k}^{2}}{1+2{k}^{2}}$,
于是:x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$-\frac{4{k}^{2}}{1+2{k}^{2}}$,y0=k(x0+2)=$\frac{2k}{1+2{k}^{2}}$ …(8分)
因为x0=$-\frac{4{k}^{2}}{1+2{k}^{2}}$≤0,所以点G不可能在y轴的右边,
又直线C1B1,C1B1方程分别为y=x+1,y=-x-1.
所以点G在正方形内(包括边界)的充要条件为
$\left\{\begin{array}{l}{{y}_{0}≤{x}_{0}+1}\\{{y}_{0}≥-{x}_{0}-1}\end{array}\right.$ 即$\left\{\begin{array}{l}{\frac{2k}{1+2{k}^{2}}≤\frac{-4{k}^{2}}{1+2{k}^{2}}+1}\\{\frac{2k}{1+2{k}^{2}}≥\frac{4{k}^{2}}{1+2{k}^{2}}-1}\end{array}\right.$ 亦即$\left\{\begin{array}{l}{2{k}^{2}+2k-1≤0}\\{2{k}^{2}-2k-1≤0}\end{array}\right.$ …(10分)
解得$-\frac{\sqrt{3}-1}{2}$≤k≤$\frac{\sqrt{3}-1}{2}$,…(2)
由(1)(2)知,直线斜率的取值范围是[$-\frac{\sqrt{3}-1}{2}$,$\frac{\sqrt{3}-1}{2}$]. …(12分)
点评 本题椭圆方程的求法,直线与椭圆的位置关系的应用,范围问题的求法,考查分类讨论思想以及转化思想的应用.

 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
| A. | a<0,b>0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a>0,b<0 |
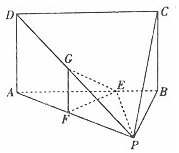 在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F、G分别为线段PA、PD的中点.
在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE:EB=7:2,点F、G分别为线段PA、PD的中点.