题目内容
6．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4，0≤x≤2}\\{2x，x＞2}\end{array}\right.$（1）求f（2），f[f（2）]的值；
（2）f（x0）=8，求x0的值．
分析 （1）由已知得f（2）=22-4=0，从而f[f（2）]=f（0），由此能求出结果．
（2）由f（x0）=8，知：当0≤x0≤2时，$f（{x}_{0}）={{x}_{0}}^{2}-4$=8，当x0＞2时，f（x0）=2x0=8，由此能求出x0的值．
解答 解：（1）∵函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4，0≤x≤2}\\{2x，x＞2}\end{array}\right.$，
∴f（2）=22-4=0，
f[f（2）]=f（0）=02-4=-4．
（2）∵f（x0）=8，
∴当0≤x0≤2时，$f（{x}_{0}）={{x}_{0}}^{2}-4$=8，
解得x0=$±2\sqrt{3}$，不合题意，舍；
当x0＞2时，f（x0）=2x0=8，
解得x0=4．
综上，x0的值是4．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
17．将函数y=sinx+cosx图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍，得到y=f（x）的图象，则y=f（x）的最小正周期为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
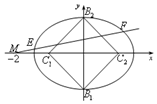已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1，过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$．