题目内容
如图，已知一艘船以30nmile/h的速度往北偏东10°的A岛行驶，计划到达A岛后停留10min后继续驶往B岛，B岛在A岛的北偏西60°的方向上．船到达C处时是上午10时整，此时测得B岛在北偏西30°的方向，经过20min到达D处，测得B岛在北偏西45°的方向，如果一切正常的话，此船何时能到达B岛？考点：解三角形的实际应用
专题：综合题,解三角形
分析：求出BD，在△ABD中，根据正弦定理，
=
=
，求出AD，AB，可得此船从C开始到B所需要的时间，即可得出结论．
| AD |
| sin15° |
| BD |
| sin110° |
| AB |
| sin55° |
解答：
解：在△BCD中，∠BCD=40°，∠BDC=180°-∠ADB=125°，CD=30×
=10（n mile），
根据正弦定理，
=
，
∴BD=
．
在△ABD中，∠ADB=45°+10°=55°，∠BAD=180°-60°-10°=110°，∠ABD=180°-110°-55°=15°．
根据正弦定理，
=
=
∴AD=
≈6.84（n mile），AB=
≈21.65（n mile）．
如果这一切正常，此船从C开始到B所需要的时间为：20+
×60+10≈86.98（min）
即约1小时26分59秒．
所以此船约在11时27分到达B岛．
| 1 |
| 3 |
根据正弦定理，
| CD |
| sin∠CBD |
| BD |
| sin∠BCD |
∴BD=
| 10×sin40° |
| sin15° |
在△ABD中，∠ADB=45°+10°=55°，∠BAD=180°-60°-10°=110°，∠ABD=180°-110°-55°=15°．
根据正弦定理，
| AD |
| sin15° |
| BD |
| sin110° |
| AB |
| sin55° |
∴AD=
| 10sin40° |
| sin70° |
| BDsin55° |
| sin110° |
如果这一切正常，此船从C开始到B所需要的时间为：20+
| AD+AB |
| 30 |
即约1小时26分59秒．
所以此船约在11时27分到达B岛．
点评：本题考查利用数学知识解决实际问题，考查正弦定理的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
已知定义在R上的函数f（x）=
若直线y=a与函数f（x）的图象恰有两个公共点，则实数a的取值范围是（ ）
|
| A、（0，2） |
| B、[0，2） |
| C、（0，2] |
| D、[1，2] |
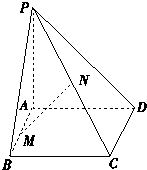如图，已知PA垂直于矩形ABCD所在的平面，M，N分别是AB，PC的中点，若∠PDA=45°，
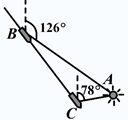如图，货轮在海上以35nmile/h的速度沿着方位角（从指北方向顺时针转到目标方向线的水平角）为148°的方向航行．为了确定船位，在B点观察灯塔A的方位角是126°，航行半小时后到达C点，观察灯塔A的方位角是78°．求货轮到达C点时与灯塔A的距离（精确到0.01nmile）．
直线l1、l2的方向向量分别为
=（1，2，-2），
=（-2，3，2），则（ ）
| a |
| b |
| A、l1∥l2 |
| B、l1与l2相交，但不垂直 |
| C、l1⊥l2 |
| D、不能确定 |