题目内容
正项数列{an}的前n项和为Sn满足:Sn2+2nSn-22n+1=0.
(1)求数列{an}的通项公式;
(2)令bn=
,数列{bn}的前n项和为Tn,证明:对于任意的n∈N*,都有Tn<2.
(1)求数列{an}的通项公式;
(2)令bn=
| 2n-1 |
| (Sn-1)(an-1) |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出Sn=2n,由此能求出an=
.
(2)当n=1时,T1=b1=1<2.当n≥2时,bn=
=
-
,由此利用裂项求和法能证明对于任意的n∈N*,都有Tn<2.
|
(2)当n=1时,T1=b1=1<2.当n≥2时,bn=
| 2n-1 |
| (2n-1)(2n-1-1) |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
解答:
(1)解:Sn2+2nSn-22n+1=0,
(Sn-2n)(Sn+2n+1)=0,解得Sn=2n
当n=1时,a1=S1=2.
当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,
∵n=1不适合,
∴an=
.
(2)证明:当n=1时,b1=
=
=1,T1=b1=1<2.
当n≥2时,bn=
=
-
Tn=1+(
-
)+(
-
)+…+(
-
)=2-
<2
综上,对于任意的n∈N*,都有Tn<2.
(Sn-2n)(Sn+2n+1)=0,解得Sn=2n
当n=1时,a1=S1=2.
当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1,
∵n=1不适合,
∴an=
|
(2)证明:当n=1时,b1=
| 21-1 |
| (S1-1)(a1-1) |
| 1 |
| (2-1)2 |
当n≥2时,bn=
| 2n-1 |
| (2n-1)(2n-1-1) |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
| 1 |
| 2-1 |
| 1 |
| 22-1 |
| 1 |
| 22-1 |
| 1 |
| 23-1 |
| 1 |
| 2n-1-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n-1 |
综上,对于任意的n∈N*,都有Tn<2.
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
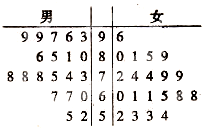 在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示:
在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示: