题目内容
在平面直角坐标系xoy中,已知曲线C的参数方程为
(α为参数).以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ-
)=2
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
|
| π |
| 4 |
| 2 |
(Ⅰ)求直线l的直角坐标方程;
(Ⅱ)点P为曲线C上的动点,求点P到直线l距离的最大值.
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)根据x=ρcosθ,y=ρsinθ,把直线l的极坐标方程化为直角坐标方程.
(Ⅱ)设点P(2cosα,sinα),求得点P到直线l距离d=
,可得d的最大值.
(Ⅱ)设点P(2cosα,sinα),求得点P到直线l距离d=
|
| ||
|
解答:
解:(Ⅰ)∵直线l的极坐标方程为ρcos(θ-
)=2
,即 ρcosθ+ρsinθ=4,
化为直角坐标方程为 x+y-4=0.
(Ⅱ)设点P(2cosα,sinα),点P到直线l距离d=
=
,
其中,sinβ=
,cosβ=
.
故当sin(α+β)=-1时,d取得最大值为
=
+2
.
| π |
| 4 |
| 2 |
化为直角坐标方程为 x+y-4=0.
(Ⅱ)设点P(2cosα,sinα),点P到直线l距离d=
| |2cosα+sinα-4| | ||
|
|
| ||
|
其中,sinβ=
| 2 | ||
|
| 1 | ||
|
故当sin(α+β)=-1时,d取得最大值为
| ||
|
| ||
| 2 |
| 2 |
点评:本题主要考查把极坐标化为直角坐标方程的方法,点到直线的距离公式、两角和差的正弦公式、正弦函数的值域,属于基础题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
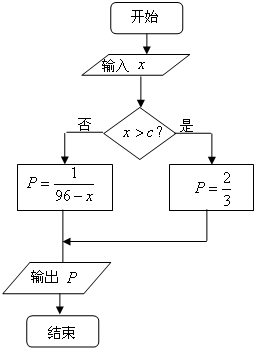 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=