题目内容
5.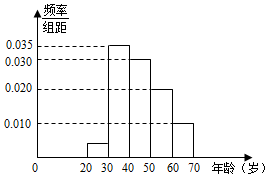 某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.
某市为庆祝北京夺得2022年冬奥会举办权,围绕“全民健身促健康,同心共筑中国梦”主题开展全民健身活动,组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组[20,30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70],得到的频率分布直方图如图所示.(Ⅰ)若电视台记者要从抽取的群众中选1人进行采访,求被采访人恰好在第1组或第4组的概率;
(Ⅱ)已知第1组群众中男性有3名,组织方要从第1组中随机抽取2名群众组成维权志愿者服务队,求至少有1名女性群众的概率.
分析 (Ⅰ)设第1组[20,30)的频率为f1,利用概率和为1,求解即可,再根据概率公式计算即可;
(Ⅱ)第1组中共有6名群众,其中女性群众共3名,记第1组中的3名男性群众分别为A,B,C,3名女性群众分别为x,y,z,根据概率公式计算即可.
解答 解:(Ⅰ)设第1组[20,30)的频率为f1,则由题意可知,
f1=1-(0.010+0.035+0.030+0.020)×10=0.05,
被采访人恰好在第1组或第4组的频率为0.05+0.020×10=0.25,
∴估计被采访人恰好在第1组或第4组的概率为0.25,
(Ⅱ)第1组[20,30)的人数为0.05×120=6,
∴第1组中共有6名群众,其中女性群众共3名,
记第1组中的3名男性群众分别为A,B,C,3名女性群众分别为x,y,z,
从第1组中随机抽取2名群众组成维权志愿者服务队,共有15个基本事件,列举如下:AB,AC,Ax,Ay,Az,BC,Bx,By,Bz,Cx,Cy,Cz,xy,xz,yz,
至少有1名女性群众Ax,Ay,Az,Bx,By,Bz,Cx,Cy,Cz,xy,xz,yz共12个基本事件,
∴从第1组中随机抽取2名群众组成维权志愿者服务队,至少有1名女性群众的概率为$\frac{12}{15}$=$\frac{4}{5}$.
点评 本题考查古典概型概率公式的应用概率的求法,考查计算能力.

练习册系列答案
相关题目
15.一个几何体的三视图如图,则该几何体的体积为( )
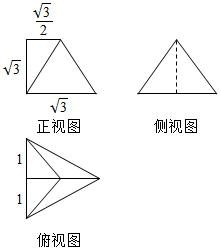

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |