题目内容
16．已知f（x）为R上的奇函数，当x＞0时，f（x）=3x，那么f（-2）的值为-9．分析 根据函数奇偶性的性质，由f（-2）=-f（2）进行求解即可．
解答 解：∵f（x）为R上的奇函数，当x＞0时，f（x）=3x，
∴f（-2）=-f（2）=-32=-9，
故答案为：-9．
点评 本题主要考查函数值的计算，根据函数奇偶性的性质进行转化是解决本题的关键．比较基础．
练习册系列答案
相关题目
9．α=-1，则α的终边所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．如图所示的程序框图，其作用是输入x的值，输出相应的y值，若输入$x=\frac{π}{2}$，则输出的y值为（ ）
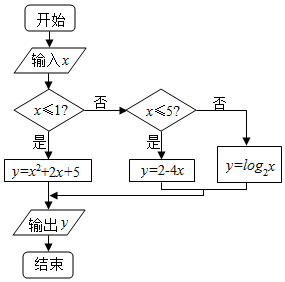
| A． | 2 | B． | ${log_2}\frac{π}{2}$ | C． | 2-2π | D． | 8 |
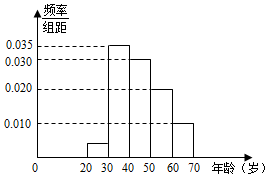某市为庆祝北京夺得2022年冬奥会举办权，围绕“全民健身促健康，同心共筑中国梦”主题开展全民健身活动，组织方从参加活动的群众中随机抽取120名群众，按他们的年龄分组：第1组[20，30），第2组[30，40），第3组[40，50），第4组[50，60），第5组[60，70]，得到的频率分布直方图如图所示．