题目内容
18.函数f(x)=$\left\{\begin{array}{l}1-x,x≤0\\{log_2}x,x>0\end{array}$,且f(a)=2,则a=-1或4.分析 利用分段函数以及方程,求解即可.
解答 解:当a≤0时,1-a=2,解得a=-1.
当a>0时,log2a=2,解得a=4.
综上a=-1或4
故答案为:-1或4.
点评 本题考查分段函数的应用,函数的零点的求法,考查计算能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.下列函数中,在(0,+∞)上为增函数的是( )
| A. | y=-x2 | B. | $y={(\frac{1}{π})^x}$ | C. | $y={log_{\frac{1}{2}}}x$ | D. | $y=\sqrt{x}$ |
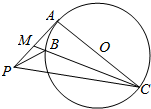 如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B.
如右图所示,PA为圆O的切线,切点为A,AC是直径,M为PA的中点,MC与圆交于点B. 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.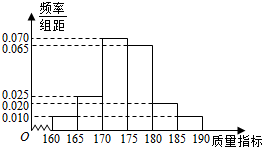 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.